Đặt z = a + bi(a, b ∈ R).
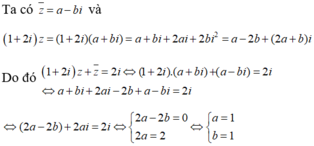
Suy ra z = 1 + i. Vậy z . z = | z | 2 = 1 2 + 1 2 = 2
Chọn B
Đặt z = a + bi(a, b ∈ R).
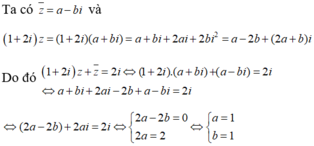
Suy ra z = 1 + i. Vậy z . z = | z | 2 = 1 2 + 1 2 = 2
Chọn B
Cho số phức z thỏa mãn ( 2 + i ) z + 2 ( 1 + 2 i ) 1 + i . Môđun của số phức w = z + i + 1 là
A. 3
B. 4
C. 5
D. 6
Cho số phức z thỏa mãn (3 + 2i)z + (2 - i)2 = 4 + i. Môđun của số phức w = ( z + 1 ) z là
A. 2
B. 4
C. 10
D. 10
Cho số phức z thỏa mãn: i . z + z = 2 + 2 i và z . z = 2 . Khi đó z 2 bằng:
A. 2
B. 4
C. – 2i
D. 2i
Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức: w = z - 2 z + 1 z 2 là
A. 2
B. 4
C. 10
D. 10
Số phức z thỏa mãn z(1 + 2i) + 1 - i = 2i là
A. -1+i
B. 1-i
C. 1+i
D. -1-i
Cho số phức z thỏa mãn 5 ( z + i ) z + 1 = 2 - i . Khi đó môđun của số phức w = 1 + z + z 2 là
A. 5
B. 13
C. 13
D. 5
Trong các số phức thỏa mãn điều kiện z - 4 i - 2 = 2 i - z , môđun nhỏ nhất của số phức z bằng:
A. 2
B. 3
C. 2 2
D. 2 3
Số phức z thỏa mãn z = ( 1 + 2 i ) 3 2 - i là
A. z = 4 - 3i
B. z = 4 + 3i
C. z = -4 - 3i
D. z = -4 + 3i
Cho số phức z thỏa mãn (2 + 3i)z = 1 Khi đó, z + 2 z bằng
A. -1+i
B. -1-i
C. 1+i
D. 1-i