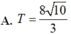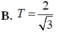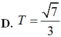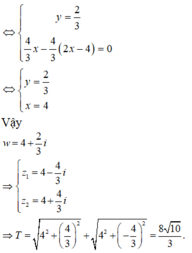Các câu hỏi tương tự
Cho các số phức z, w khác 0 và thỏa mãn |z-w| 2|z| |w| Phẩn thực của số phức
u
z
w
là:
Đọc tiếp
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w| Phẩn thực của số phức u = z w là:
![]()
![]()
![]()
![]()
Cho số phức z, w khác 0 sao cho |z-w| 2|z| |w|. Phần thực của số phức
u
z
w
là A. a -
1
8
B. a
1
4
C. a 1 D. a
1
8
Đọc tiếp
Cho số phức z, w khác 0 sao cho |z-w| = 2|z| = |w|. Phần thực của số phức u = z w là
A. a = - 1 8
B. a = 1 4
C. a = 1
D. a = 1 8
Cho số phức z thay đổi hoàn toàn thỏa mãn: |z-i| = |z-1+2i|. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (2-i)z+1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. -x + 7y + 9 = 0
B. x + 7y - 9 = 0
C. x + 7y + 9 = 0
D. x - 7y + 9 = 0
Biết số phức
z
≠
0 và w
z
1
-
i
. Biết A,B là các điểm biểu diễn của z,w thì: A.
∆
ABO đều B.
∆
ABO vuông cân C. O là trung điểm AB D.
∆
ABO có một góc
30
0
Đọc tiếp
Biết số phức z ≠ 0 và w = z 1 - i . Biết A,B là các điểm biểu diễn của z,w thì:
A. ∆ ABO đều
B. ∆ ABO vuông cân
C. O là trung điểm AB
D. ∆ ABO có một góc 30 0
Cho z là số phức thỏa mãn điều kiện
2
z
−
1
1
+
i
+
z
¯
+
1
1
−
i
2
−
2
i
. Tính tổng bình phương phần thực và phần...
Đọc tiếp
Cho z là số phức thỏa mãn điều kiện 2 z − 1 1 + i + z ¯ + 1 1 − i = 2 − 2 i . Tính tổng bình phương phần thực và phần ảo của số phức w = 9 z 2 + 6 z + 1
A. 25
B. 1
C. 49
D. 41
Biết phương trình
z
2
+
a
z
+
b
0
(
b
,
c
∈
R
)
có một nghiệm z1-i. Tính môđun của số phức wa+bi.
Đọc tiếp
Biết phương trình z 2 + a z + b = 0 ( b , c ∈ R ) có một nghiệm z=1-i. Tính môđun của số phức w=a+bi.
![]()
![]()
![]()
![]()
Cho số phức thỏa mãn
z
-
i
z
-
1
+
2
i
. Tập hợp điểm biểu diễn số phức w (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
Đọc tiếp
Cho số phức thỏa mãn z - i = z - 1 + 2 i . Tập hợp điểm biểu diễn số phức w = (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
![]()
![]()
![]()
![]()
Cho các số phức z thỏa mãn
z
+
1
2
. Biết rằng tập hợp các điểm biểu diễn các số phức
w
(
1
+
i
8
)
z
+
i
là một đường tròn. Bán kính r của đường tròn đó là
Đọc tiếp
Cho các số phức z thỏa mãn z + 1 = 2 . Biết rằng tập hợp các điểm biểu diễn các số phức w = ( 1 + i 8 ) z + i là một đường tròn. Bán kính r của đường tròn đó là
![]()
![]()
![]()
![]()
Cho các số phức z thỏa mãn
z
−
i
z
−
1
+
2
i
. Tập hợp các điểm biểu diễn số phức
w
2
−
i
z
+
1
trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là A....
Đọc tiếp
Cho các số phức z thỏa mãn z − i = z − 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = 2 − i z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x − 7 y − 9 = 0
B. x + 7 y − 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0
Có bao nhiêu phát biểu sau là đúng (z, w là các số phức): (*)
z
w
¯
thì
z
¯
w
(*) z
-
w
¯
→
z
¯
-
w
(*)
z
3
w...
Đọc tiếp
Có bao nhiêu phát biểu sau là đúng (z, w là các số phức):
(*) z = w ¯ thì z ¯ = w
(*) z = - w ¯ → z ¯ = - w
(*) z 3 = w 3 → z = w
(*) z 6 = 1 thì có 6 nghiệm phức
(*) z = w ¯ ⇔ z , w ∈ ℝ
A. 2 phát biểu
B. 3 phát biểu
C. 4 phát biểu
D. 5 phát biểu