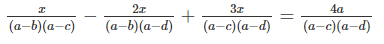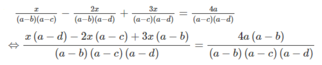
⇔ x(a − d) − 2x(a − c) + 3x(a − b) = 4a(a − b)
⇔ x(a − d − 2a + 2c + 3a − 3b) = 4a(a − b)
⇔ x(2a − 3b + 2c − d) = 4a(a − b)
Theo giả thiết, b + d = 2c nên 2a – 3b + 2c – d = 2a – 2b = 2 (a – b ).
Do đó phương trình đã cho tương đương với phương trình 2(a − b)x = 4a(a − b)
Để ý rằng a – b ≠ 0, ta thấy ngay phương trình cuối có nghiệm duy nhất x = 2a.
Vậy phương trình đã cho cũng có nghiệm duy nhất x = 2a.