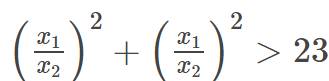Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì: $\Delta=k^2-8\geq 0$
$\Leftrightarrow k^2\geq 8(1)$
Áp dụng định lý Viet:
$x_1+x_2=-k$
$x_1x_2=2$
Khi đó:
$(\frac{x_1}{x_2})^2+(\frac{x_2}{x_1})^2> 23$
$\Leftrightarrow \frac{x_1^4+x_2^4}{(x_1x_2)^2}>23$
$\Leftrightarrow x_1^4+x_2^4> 23(x_1x_2)^2=23.2^2=92$
$\Leftrightarrow (x_1^2+x_2^2)^2-2(x_1x_2)^2> 92$
$\Leftrightarrow (x_1^2+x_2^2)^2-8> 92$
$\Leftrightarrow [(x_1+x_2)^2-2x_1x_2]^2>100$
$\Leftrightarrow (k^2-4)^2>100$
$\Leftrightarrow k^2-4>10$ hoặc $k^2-4<-10$
$\Leftrightarrow k^2>14$ hoặc $k^2<-6$ (loại)
$\Leftrightarrow k> \sqrt{14}$ hoặc $k< -\sqrt{14}$
Kết hợp với $k^2\geq 8$ suy ra $k> \sqrt{14}$ hoặc $k< -\sqrt{14}$