Đáp án là B
Đặt ![]()
![]()
Ta có
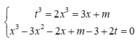
![]()
Xét hàm số
![]()
![]()
Do đó hàm số liên tục và đồng biến trên ℝ
![]()
![]()
Xét ![]()
![]()
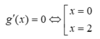
Bảng biến thiên

Từ bảng biến thiên suy ra -5 < -m < -1
![]()
Vậy tổng các phần tử của S bằng 9.
Đáp án là B
Đặt ![]()
![]()
Ta có
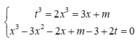
![]()
Xét hàm số
![]()
![]()
Do đó hàm số liên tục và đồng biến trên ℝ
![]()
![]()
Xét ![]()
![]()
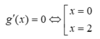
Bảng biến thiên

Từ bảng biến thiên suy ra -5 < -m < -1
![]()
Vậy tổng các phần tử của S bằng 9.
Cho phương trình log 2 2 x - 4 log 2 x - m 2 - 2 m + 3 = 0 .
Gọi S là tập hợp tất cả các giá trị thực của tham số m để phương trình có hai nghiệm thực phân biệt x 1 , x 2 thỏa mãn x 1 2 + x 2 2 = 68 . Tính tổng các phần tử của S
A. -1
B. -2
C. 1
D. 2
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 - x + 1 - x = m + x - x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11.
B. 0.
C. 5.
D. 6.
Gọi S là tập chứa các giá trị nguyên của m để phương trình e 3 x 3 - 18 x + 30 - m + e x 3 - 6 x + 10 - m - e 2 m = 1 có 3 nghiệm thực phân biệt. Tính tổng các phần tử của tập S
A. 110
B. 106
C. 126
D. 24
Gọi S là tập chứa các giá trị nguyên của m để phương trình e 3 x 3 - 18 x + 30 - m + e x 3 - 6 x + 10 - m - e 2 m = 1 có 3 nghiệm thực phân biệt. Tính tổng các phần tử của tập S.
A.110
B.106
C.126
D.24
Cho hàm số y = ax 3 + bx 2 + cx + d với a ≠ 0 có hai hoành độ cực trị là x=1 và x=3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) = f(m) có đúng ba nghiệm phân biệt là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = a x 3 + b x 2 + c x + d với a khác 0 có hai hoành độ cực trị là x=1 và x=3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) = f(m) có đúng ba nghiệm phân biệt là:
![]()
![]()
![]()
![]()
Gọi S là tập tất cả các giá trị nguyên của tham số m với m < 64 để phương trình log 1 5 x + m + log 5 2 - x = 0 có nghiệm. Tính tổng tất cả các phần tử của S .
A. 2018
B. 2016
C. 2015
D. 2013
Gọi S là tập hợp các giá trị nguyên của m để phương trình x 2 + y 2 + z 2 - 2 ( m + 2 ) x + 4 m y - 2 m z + 7 m 2 - 1 = 0 là phương trình mặt cầu. Số phần tử của S là
A. 6
B. 7
C. 4
D. 5
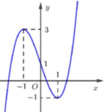
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) = 2sin x +m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng:
A. -10
B. -8
C. -6
D. -5