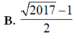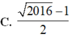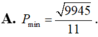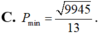Question

Cho phương trình  8z² - 4(a + 1)z + 4a + 1 = 0 (1) với a là tham số. Tính tổng tất cả các giá trị của a để (1) có hai nghiệm z₁; z₂  thỏa mãn  z₁/ z₂  là số ảo, trong đó z₂ là số phức có phần ảo dương.

A. 1

B. 2

C. 3

D. 4

Answer 1

Chọn B.

Từ giả thiết suy ra z₁; z₂ không phải là số thực.

Do đó Δ’ < 0, hay  4( a + 1)² - 8(4a + 1) < 0

Hay a² - 6a -1 < 0    (*)

Suy ra ,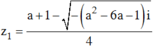 

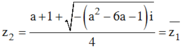
Ta có z₁/ z₂ là số ảo khi và chỉ khi  là số ảo

Tương đương: (a + 1)² - (-(a² - 6a - 1)) = 0 hay a² - 2a = 0

Vậy a = 0 hoặc a = 2.

Đối chiếu với điều kiện (*) ta có giá trị của a là a = 0 hoặc a = 2.