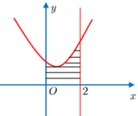
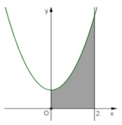
Phương trình hoành độ giao điểm của (P) và d là x 2 - m x - 1 = 0
Ta có ∆ = m 2 + 4 > 0 ∀ m . Suy ra phương trình luôn có 2 nghiệm phân biệt x 1 ; x 2
Giả sử x 1 < x 2 . Khi đó:
S = ∫ x 1 x 2 m x + 2 - x 2 - 1 d x = ∫ x 1 x 2 m x + 1 - x 2 d x = m 2 + 4 m 2 6 + 2 3 ≥ 4 3
Vậy m i n S = 4 3 ⇔ m = 0
Đáp án D