Tương tự câu 3
Chứng minh được A O B ^ = 120 0
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
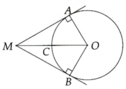
Cho ( O ; 5cm ) và điểm M sao cho OM = 10cm . Vẽ hai tiếp tuyến MA và MB . Tính góc ở tâm di hai tia OA và OB tạo ra
Cho (0;5 cm ) và điểm M sao cho OM=10cm. vẽ hai tiếp tuyến MA và MB. Tính góc ở tâm do 2 tia OA và OB tạo ra.
Từ một điểm M ở ngoài (O;R) sao cho OM=2R. Vẽ hai tiếp tuyến MA,MB (A,B là tiếp điểm) ,gọi H là giao điểm OM và AB.
a) Cm: OH vuông góc AB và tính HM theo R.
b) Cm: 4 điểm M,A,O,B thuộc 1 đường tròn, ác địch tâm I của đường tròn.
c) Tia OI cắt (O;R) tại C. Cm MC.IH=MI.HC
Cho đường tròn tâm O bán kính 5cm. Từ điểm M nằm ngoài (O) vẽ tiếp tuyến MA (A là tiếp điểm).
a/ Biết OM = 10 cm. Tính AM.
b/ Kẻ AH vuông góc OM tại H, tia AH cắt đường tròn (O) tại B. Chứng minh tam giác ABM cân..
c/ Chứng minh MB là tiếp tuyến của đường tròn (O)
Bài 1: Cho đường tròn (O, R) và điểm M nằm ngoài đường tròn đó. Gọi MA, MB là hai tiếp tuyến với đường tròn tại A và B. Tính số đo của góc ở tâm tạo bởi hai bán kính OA và OB nếu:
a) ∠AMB = 70o
b) MA = R
c) MO = 2R
Bài 5: Từ điểm M nằm ngoài đường tròn (O), kẻ tiếp tuyến MA và cát tuyến MCD sao cho MD nằm giữa hai tia MA và MO. a)Cm: MA?= MC.MD b)Vẽ dây AB vuông góc với OM tại H. Cm: MB là tiếp tuyến của đường tròn (O) c)Cm: MH.MO = MC.MD và MHC = MDÒ
Cho đường tròn (O; 3 cm) và một điểm M sao cho OM = 5cm. Từ M kẻ tiếp tuyến MA,MB với đường tròn (O) (A và B là hai tiếp điểm). Gọi I là giao điểm của OM và ABa) Tính độ dài đoạn AM và giá trị tan của góc AMO
Xem chi tiết
b) Chứng minh OM⊥AB tại I
c)Từ B kẻ đường kính BC của đường tròn (O), đường thẳng MC cắt đường tròn (O) tại D (D≠C). Chứng minh ΔMDO đồng dạng với ΔMIC
Cho đường tròn (O; R) và hai tiếp tuyến MA, MB cắt nhau tại M (A, B là các tiếp tuyến điểm). a) Chứng minh rằng OM vuông góc AB. b) Gọi H là giao điểm của OM và AB. Cho bán kính dường tròn bằng 13cm, OH = 5cm Tính độ dàiAB.
Cho đường tròn (O;R) và điểm M nằm ngoài (O) sao cho OM=2R. Vẽ các tiếp tuyến MA,MB đến đường tròn (A,B là hai tiếp điểm)
a, Cm tgiac MAB là tgiac đều
b, Tính Smab theo R
c, Tia MO cắt (O) tại H và K (H nằm giữa M,K). Từ O vẽ ON vg góc với AK. CM B,O,N thẳng hàng