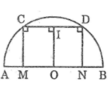
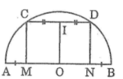
Ta có: CM ⊥ CD
DN ⊥ CD
Suy ra: CM // DN
Kẻ OI ⊥ CD
Suy ra: OI // CM // DN
Ta có: IC = ID (đường kính dây cung)
Suy ra: OM = ON (1)
Mà: AM + OM = ON + BN (= R) (2)
Từ (1) và (2) suy ra: AM = BN
Cho nửa đường tròn (O) đường kính AB , dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB tại M và N. Chứng Minh rằng AM=BN
Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho AM = BN. Qua M và N kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD.
Cho nửa đường tròn tâm O đường kính AB, dây CD các đường vuông góc với C,D tại C, D cắt AB ở E, F
a, Chứng minh rằng E đối xứng với F qua O
b, tính S tứ giác CDFE biết AB=5 cm CD=14cm
Cho nữa đường tròn tâm O đường kính AB . Trên AB lấy hai điểm M và N sao cho AM = BN . Qua M và N kẻ hai đường thẳng song song với nhau cắt nửa đường tròn lần lượt ở C và D . Chứng minh rằng MC và ND vuông góc với CD
#giải giúp với ạ đang bí k biết làm thế nào ?
Cho đường tròn tâm O dây AB. Trên cung AB lần lượt lấy M,N. Hai đường thẳng AM và NB cắt nhau tại C, hai đường thẳng AN và MB cắt nhau tại D. Cho biết góc ACN = góc ADM. Chứng minh rằng: AB vuông góc với CD
Cho nửa đường tròn đường kính AB và một dây CD. Qua C vẽ đường thẳng vuông góc với CD, cắt AB tại I. Các tiếp tuyến tại A và B của nửa đường tròn cắt đường thẳng CD theo thứ tự tại E và F. Chứng minh rằng: Tam giác IEF vuông
Cho nửa đường tròn (O) đường kính AB, dây CD không cắt AB. Các đường vuông góc với CD tại C và D cắt AB tại E và F
a) Chứng minh rằng E và F đối xứng với nhau qua O
Tính \(S_{CDFE}\)biết AB=50cm; CD=14cm
Cho nửa đường tròn đường kính AB và một dây CD. Qua C vẽ đường thẳng vuông góc với CD, cắt AB tại I. Các tiếp tuyến tại A và B của nửa đường tròn cắt đường thẳng CD theo thứ tự tại E và F. Chứng minh rằng: Các tứ giác AECI và BFCI nội tiếp được
Cho đường tròn tâm O, đường kính AB. Dây CD cắt đường kính AB tại I. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK
