Question

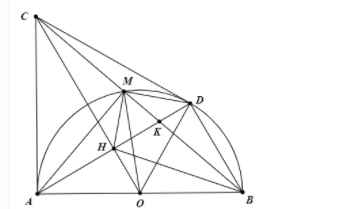
Cho nửa đường tròn $(O ; R)$, đường kính $A B$. Trên tia tiếp tuyến kẻ từ $A$ của nửa đường tròn này lấy $C$ sao cho $A C>R .$ Từ $C$ kẻ tiếp thứ hai $C D$ của nửa đường tròn $(O ; R)$, với $D$ là tiếp Gọi $H$ là giao điểm của $A D$ và $O C$.

1) Chứng minh: $A C D O$ là tứ giác nội tiếp.

2) $B C$ cắt đường tròn $(O ; R)$ tại điểm thứ hai là $M$. Chứng minh: $C D^{2}=C M . C B .$

3) Gọi K là giao điểm của AD và BC. Chứng minh \(\widehat{MHC}=\widehat{CBO}\) và \(\dfrac{CM}{CB}=\dfrac{KM}{KB}\).

Answer 1

1. Xét nửa đường tròn (O) , có:


AC, CD là 2 tiếp tuyến của nửa đường tròn (O) (tiếp điểm A, D) (gt)


=> CA = CD , \(\widehat{CAO}=\widehat{CDO}=90^o\)

Xét tứ giác CAOD, có:


\(\widehat{CAO}+\widehat{CDO}=90^o+90^o=180^o\)

\(\widehat{CAO}\)và \(\widehat{CDO}\)là 2 góc đối nhau


=> ACDO là tứ giác nội tiếp 


 

Answer 2

Xét \(\Delta CDM\)và \(\Delta CBD\), có:

\(\widehat{MCD}chung\)

\(\widehat{CDM}=\widehat{CBD}\)(góc nội tiếp và góc tạo bời tia tiếp tuyến và dây cung cùng chắn \(\widebat{MD}\) ) 

\(\Rightarrow\Delta~\Delta\left(gg\right)\)

\(\Rightarrow\frac{CD}{CB}=\frac{CM}{CD}\Leftrightarrow CD^2=CM.CB\)

Answer 3

Câu a:

Có góc CAO= góc ODC= 90 độ (vì AC và CD là tt)

      Mà 2 góc lại ở vị trí đối nhau

    ⇒ Tứ giác ACDO nội tiếp

Câu b:

    Xét \(\Delta CDM\) và \(\Delta CBD\) có:

           Góc C chung

           Góc CDM= góc CBD ( cùng chắn cung MD)

    → \(\Delta CDM\) đồng dạng \(\Delta CBD\) (góc góc )

            ⇒\(\dfrac{CD}{CM}\)=\(\dfrac{CB}{CD}\) ⇔ CD²=CM.CB

 

Answer 4

Answer 5

Answer 6

Answer 7

 

 

Answer 8

1) Tứ giác $ACDO$ có $\widehat{CAO}=\widehat{CDO}={90}^{\circ }$ (tính chất của tiếp tuyến ) nên tử giác $ACDO$ nội tiếp đường tròn đường kính $AO$.

2) Xét $\Delta CDM$ và $\Delta CBD$ có: $\widehat{MCD}$ chung: $\Rightarrow \Delta CDM\backsim \Delta CBD\Rightarrow \frac{CD}{CM}=\frac{CB}{CD}\iff C{D}^2=CM\cdot CB$

3) Theo tính chất hai tiếp tuyến cắt nhau, ta có $CA=CD$ mà $OA=OD(=R)$ nên $OC$ là trung trực của $AD\Rightarrow OC\perp AD$ tại trung điểm 

Đúng 0

Bình luận (0)

Answer 9

1) Tứ giác $ACDO$ có $\widehat{CAO}=\widehat{CDO}={90}^{\circ }$ (tính chất của tiếp tuyến ) nên tử giác $ACDO$ nội tiếp đường tròn đường kính $AO$.

2) Xét $\Delta CDM$ và $\Delta CBD$ có: $\widehat{MCD}$ chung: $\Rightarrow \Delta CDM\backsim \Delta CBD\Rightarrow \frac{CD}{CM}=\frac{CB}{CD}\iff C{D}^2=CM\cdot CB$

3) Theo tính chất hai tiếp tuyến cắt nhau, ta có $CA=CD$ mà $OA=OD(=R)$ nên $OC$ là trung trực của $AD\Rightarrow OC\perp AD$ tại trung điểm 

Đúng 0

Bình luận (0)