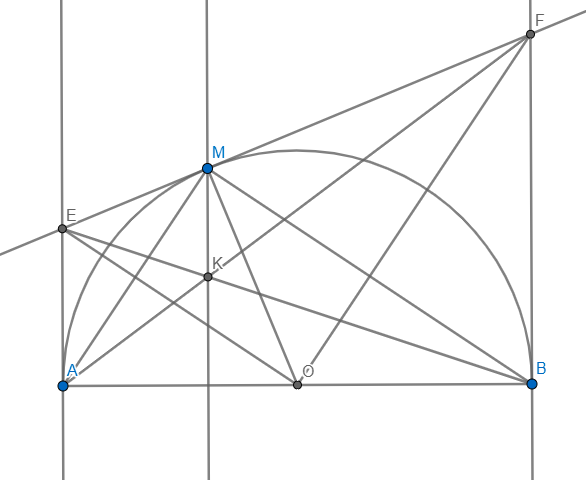
Cho nửa đường tròn (O) đường kính AB = a. Gọi Ax, By là các tia vuông góc với AB ( Ax, By thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (O) (M khác A và B) kẻ tiếp tuyến với nửa đường tròn (O); nó cắt Ax, By lần lượt ở E và F.
1. Chứng minh: góc EOF = 90o
2. Chứng minh tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.
3. Gọi K là giao điểm của AF và BE, chứng minh MK vuông góc AB.
1) Vì EM,EA là tiếp tuyến \(\Rightarrow OE\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOE=\dfrac{1}{2}\angle MOA\)
Vì FM,FB là tiếp tuyến \(\Rightarrow OF\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOB\)
\(\Rightarrow\angle MOE+\angle MOF=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)=\dfrac{1}{2}.180=90\)
\(\Rightarrow\angle EOF=90\)
2) Ta có: \(\angle EAO+\angle EMO=90+90=180\Rightarrow AEMO\) nội tiếp
\(\Rightarrow\angle MEO=\angle MAO\)
Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
Xét \(\Delta MAB\) và \(\Delta OEF:\) Ta có: \(\left\{{}\begin{matrix}\angle AMB=\angle EOF\\\angle FEO=\angle MAB\end{matrix}\right.\)
\(\Rightarrow\Delta MAB\sim\Delta OEF\left(g-g\right)\)
Vì \(AE\parallel BF(\bot AB)\) \(\Rightarrow\dfrac{BF}{AE}=\dfrac{FK}{AK}\left(1\right)\)
Vì EM,EA là tiếp tuyến \(\Rightarrow EA=EM\left(2\right)\)
Vì FM,FB là tiếp tuyến \(\Rightarrow FB=FM\left(3\right)\)
Thế (2),(3) vào (1) \(\Rightarrow\dfrac{FM}{EM}=\dfrac{FK}{AK}\Rightarrow\) \(MK\parallel AE\) \(\Rightarrow MK\bot AB\)