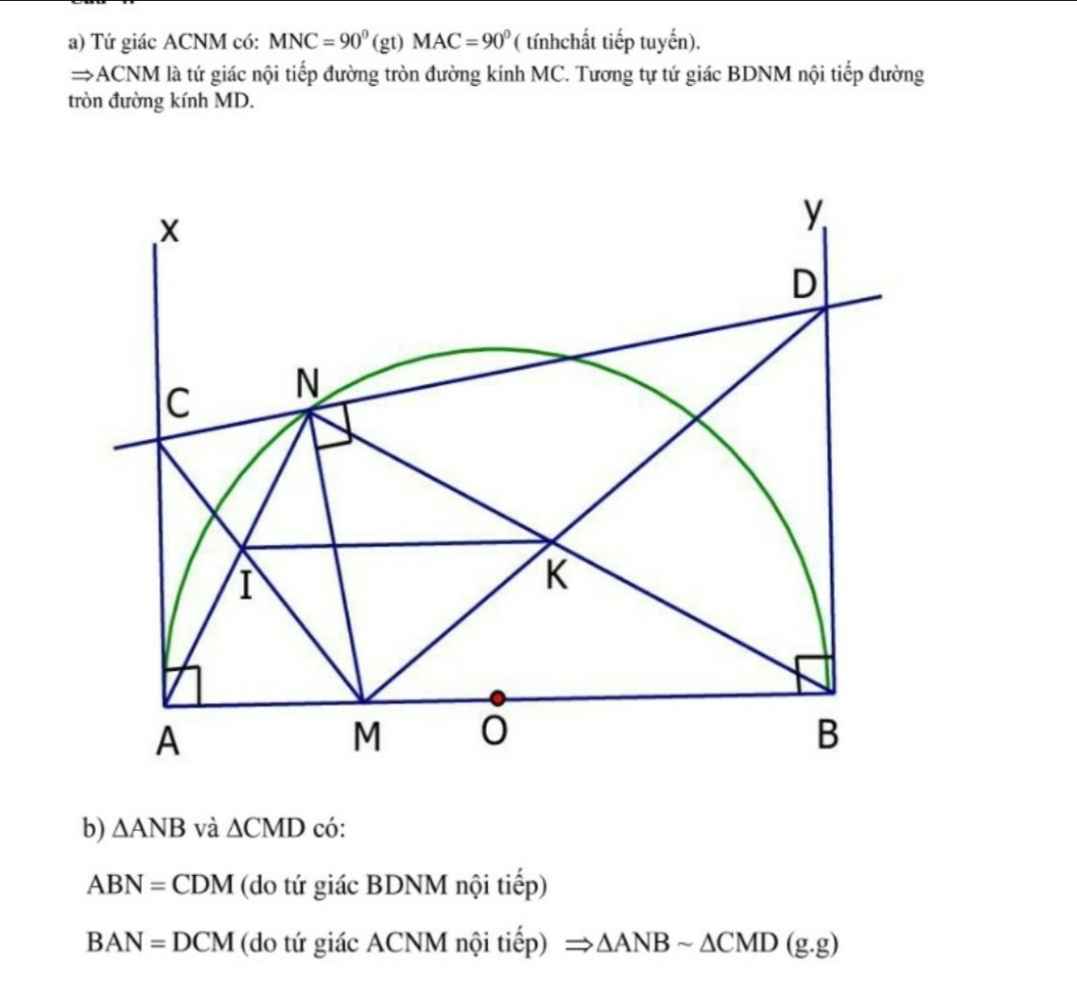
Cho nửa đường tròn tâm O đường kính AB. Lấy điểm M thuộc đoạn thẳng OA, điểm N thuộc nửa đường tròn (O). Từ A và B vẽ các tiếp tuyến Ax và By. Đường thẳng qua N và vuông góc với NM cắt Ax, By thứ tự tại C và D.
a) Chứng minh ACNM và BDNM là các tứ giác nội tiếp đường tròn.
b) Chứng minh ∆ANB đồng dạng với ∆CMD.
\(a,\\ \widehat{CAM}=\widehat{CNM}=90^0\\ \Rightarrow CNMA.là,tứ.giác.nội.tiếp\\ \widehat{MND}=\widehat{MBD}=90^0\\ \Rightarrow NMBF.là.tứ,giác.nội.tiếp\\ b,CNMA.nội.tiếp\\ \Rightarrow\widehat{NAM}=\widehat{NCM}\\ MNDB.nội.tiếp\\ \Rightarrow\widehat{NDM}=\widehat{NBM}\)
\(\Delta CMD.và.\Delta AnpNB:\\ \widehat{NAM}=\widehat{NCM};\widehat{NDM}=\widehat{ABM}\\ \Rightarrow\Delta....đồng.dạng.\Delta....\)