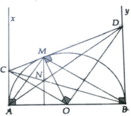
Cho nửa đường tròn (O) đường kính AB = 2R. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. M là điểm trên (O) sao cho tiếp tuyên tại M cắt Ax, By tại D và C. Đường thẳng AD cắt BC tại N
a, Chứng minh A, C, M, O cùng thuộc một đường tròn. Chỉ ra bán kính của đường tròn đó
b, Chứng minh OC và BM song song
c, Tìm vị trí điểm M sao cho SACDB nhỏ nhất
d, Chứng minh MN và AB vuông góc nhau
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB

