Cho nửa đường tròn đường kính A B = 2 R và một điểm C thay đổi trên nửa đường tròn đó, đặt C A B = α và gọi H là hình chiếu vuông góc của C trên AB. Tìm α sao cho thể tích của vật thể tròn xoay tạo thành khi xoay tam giác ACH quanh trục AB đạt giá trị lớn nhất:
A. α = 60 °
B. α = 45 °
C. α = arctan 1 2
D. α = 30 °
Đáp án C
Phương pháp:
- Tính thể tích khối nón có được khi quay tam giác ACH quanh AB (hay AH) bằng công thức V = 1 3 S d . h với đáy là hình tròn tâm H bán kính CH và chiều cao là AH.
- Tìm GTLN của thể tích dựa vào phương pháp xét hàm, từ đó tìm được AH.
Cách giải: Thể tích khối nón khi quay
Δ
A
C
H
quay quanh AB:
V = 1 3 A H . π . C H 2 = 1 3 A H . π . A H . A B − A H 2 = 2 R π 3 . A H 2 − π 3 A H 3
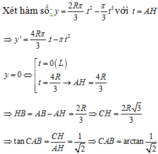
Chú ý khi giải:
Ở bước kết luận nhiều HS sẽ kết luận sai góc α là góc 45 ° dẫn đến chọn sai đáp án.

