Đáp án B
Phương pháp: Viết phương trình dao động và dựa vào tính chất lượng giác.
Cách giải: Ta có phương trình dao động của M và N là:

Dễ thấy hai dao động vuông pha, nên ta có :
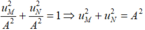
Đáp án B
Phương pháp: Viết phương trình dao động và dựa vào tính chất lượng giác.
Cách giải: Ta có phương trình dao động của M và N là:

Dễ thấy hai dao động vuông pha, nên ta có :
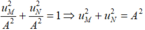
Một sóng cơ học lan truyền dọc theo một đường thẳng với biên độ sóng không đổi có phương trình sóng tại nguồn O là: u = A.cos(ωt – π/2) (cm). Một điểm M cách nguồn O bằng 1/3 bước sóng, ở thời điểm t = π ω có ly độ (cm). Biên độ 3 A là
A. 2 (cm).
B. 2 3 (cm).
C. 4 (cm).
D. 3 (cm).
Hai điểm M và N cùng nằm trên một phương truyền sóng cách nhau λ 3 ( λ là bước sóng), sóng có biên độ A và chu kỳ T. Sóng truyền từ N đến M. Giả sử ở thời điểm t 1 , hai điểm M, N có li độ lần lượt là u M = 3 c m ; u N = − 3 c m . Ở thời điểm t 2 liền ngay sau đó, có u M = + A . Hãy xác định biên độ A và thời điểm t 2 ?
A. A = 2 3 c m ; t 2 = t 1 + 11 T 12
B. A = 6 c m ; t 2 = t 1 + 11 T 12
C. A = 6 c m ; t 2 = t 1 + T 6
D. A = 2 3 c m ; t 2 = t 1 + T 6
Hai điểm M và N nằm trên cùng một phương truyền sóng cách nhau λ 3 ( λ là bước sóng), sóng có biên độ A và chu kỳ T. Sóng truyền từ N đến M. Giả sử ở thời điểm t 1 , hai điểm M, N có li độ lần lượt là u M = 3cm và u N = -3cm. Ở thời điểm t 2 liền ngay sau đó có u M = +A. Hãy xác định biên độ A và thời điểm t 2 ?
A. A = 2 3 c m , t 2 = t 1 + 11 T 12
B. A = 6 c m , t 2 = t 1 + 11 T 12
C. A = 6 c m , t 2 = t 1 + T 6
D. A = 2 3 c m , t 2 = t 1 + T 6
Cho một sóng cơ lan truyền trong môi trường với biên độ không đổi. Cho hai điểm M, N trên cùng phương truyền sóng, cách nhau λ / 3 . Tại thời điểm t li độ sóng tại M và N lần lượt là 3cm và – 3cm. Biên độ sóng:
A. 2 6 cm
B. 2 3 cm
C. 6 cm
D. 3 2 cm
Một sóng cơ truyền trên một sợi dây rất dài từ một đầu dây với biên độ không đổi là 4 mm, tốc độ truyền sóng trên dây là 2,4 m/s, tần số sóng là 20 Hz. Hai điểm M và N trên dây cách nhau 37 cm, sóng truyền từ M đến N. Tại thời điểm t, sóng tại M có li độ -2 mm và M đang đi về vị trí cân bằng. Vận tốc dao động của điểm N ở thời điểm t - 89 80 s là
A. 16 π c m / s
B. - 8 3 πcm / s
C. 80 3 πmm / s
D. -8π cm/s
Ở mặt thoáng chất lỏng có hai nguồn sóng kết hợp dao động với phương trình u A = u B = a cos 10 π t (với u tính bằng mm, t tính bằng s). Coi biên độ sóng không đổi, tốc độ truyền sóng v = 30 c m / s . Hai điểm M và N cùng nằm trên một elip nhận A, B là tiêu điểm có M A − M B = 2 c m và N A − N B = 6 c m . Tại thời điểm li độ dao động của phần từ chất lỏng tại M là 2 m m thì li độ dao động của phần tử chất lỏng tại N là:
A. 1 c m
B. − 2 2 m m
C. − 1 m m
D. 2 m m
Hai điểm M, N cùng nằm trên cùng một phương truyền sóng cách nhau x = λ 3 , sóng có biên độ A, chu kỳ T. Tại thời điểm t1 = 0, có u M = + 3 c m và u N = - 3 c m . Ở thời điểm t2 liền sau đó có uM = A. Biết sóng truyền từ N đến M. Biên độ sóng A và thời điểm t2 là
A. ![]()
B. 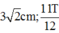
C. 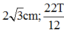
D. ![]()
Một nguồn sóng truyền từ nguồn O theo chiều dương của trục Ox có bước sóng λ = 20 cm . Phương trình dao động của nguồn O là u = 5 cos 10 πt cm . Biết biên độ sóng truyền đi không đổi. Xét hai phần tử ở M, N nằm trên trục Ox, N cách M một khoảng 5 cm theo chiều dương của trục. Ở thời điểm t1 li độ của phần tử ở M là 3cm. Ở thời điểm t 2 = t 1 + 0 , 1 (s), li độ phần tử tại N có độ lớn là
A. 2 cm.
B. 1,5 cm.
C. 3 cm.
D. 4 cm
Tại nguồn O, phương trình dao động của sóng là u = acosωt , gọi λ là bước sóng, v là tốc độ truyền sóng. Hai điểm M, N nằm trên phương truyền sóng cách nhau một đoạn d sẽ dao động lệch pha nhau một góc:
A. Δ φ = 2 π d λ
B. Δ φ = 2 π d v
C. Δ φ = π d λ
D. Δ φ = 2 π v λ