a: Xét tứ giác NCHD có
góc NCH=góc NDH=góc DNC=90 độ
nên NCHD là hình chữ nhật
b: \(S_{MNP}=\dfrac{NH\cdot MP}{2}=\dfrac{MN\cdot NP}{2}\)
nên NH*MP=MN*NP
c: \(MP=\sqrt{6^2+8^2}=10\left(cm\right)\)
=>NH=6*8/10=4,8cm
=>CD=4,8cm
a: Xét tứ giác NCHD có
góc NCH=góc NDH=góc DNC=90 độ
nên NCHD là hình chữ nhật
b: \(S_{MNP}=\dfrac{NH\cdot MP}{2}=\dfrac{MN\cdot NP}{2}\)
nên NH*MP=MN*NP
c: \(MP=\sqrt{6^2+8^2}=10\left(cm\right)\)
=>NH=6*8/10=4,8cm
=>CD=4,8cm
Cho hình chữ nhật ABCD. Từ A và C kẻ AE và CF vuông góc với BD tại E và F.
a) Chứng minh 2 đa giác ABCFE và ADCFE có diện tích bằng nhau
b) Tính diện tích của hai đa giác nói trên nếu các cạnh của hơn tỉ lệ với 4 và 3. Chu vi của hơn là 56cm.
Tính diện tích của hình được cho trong mỗi trường hợp sau đây :
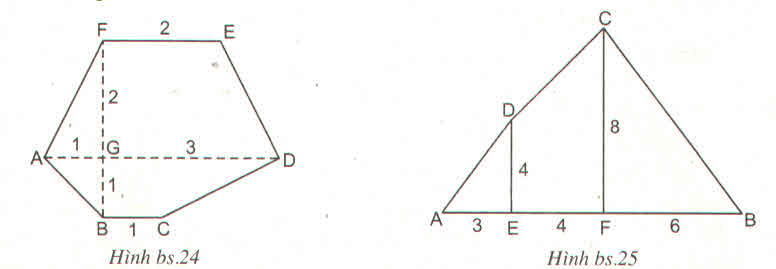
a) Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs.24
b) Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs.25)
Biết AB = 13 cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD
Cho tam giác ABC vuông tại A, AF = 1,62cm; HC = 2,5cm, GC = 2cm, BD = 1,5cm;
BA = 3,7 cm. Biết tam giác BDE đều, HG vuông góc với GC, tính diện tích đa giác DEGHF.
Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs.26
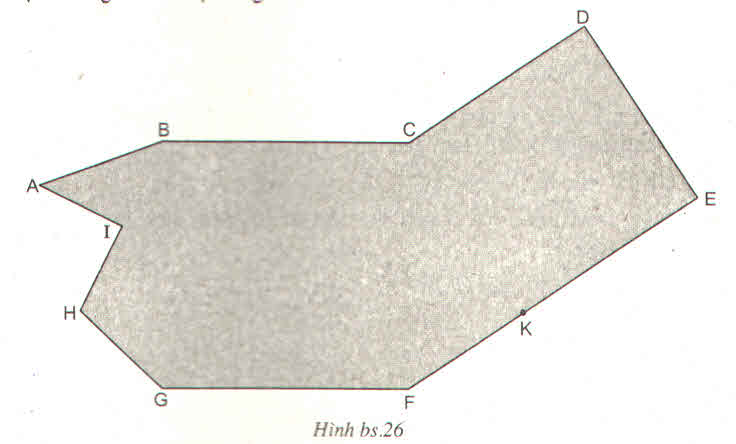
Tính diện tích của đa giác đó, biết rằng : KH song song với BC (K thuộc EF); BC song song với GF; CF song song với BG; BG vuông góc với GF; CK song song với DE; CD song song với FE; KE = DE và KE vuông góc với DE; I là trung điểm của BH; AI = IH và AI vuông góc với IH; HK = 11 cm; CF = 6cm. HK cắt CF tại J và JK = 3cm, JF = 2cm. BG cắt HK tại M và HM = 2cm
Cho hình thang cân ABCD (có AB song song với CD, AB nhỏ hơn CD)
các đường cao AH và BK
a) Tứ giác ABKH là hình gì
b) Chứng minh DH = CK
c) Gọi E là điểm đối xứng với D qua H. Chứng minh ABCE là hình bình hành
d) Tính diện tích hình tam giác ADH, tứ giác ABKH biết AB = 6cm, AH = 4cm và DH = 3cm
cứu vs
Cho hình thang ABCD (AB // Cd) có AD= 6cm, góc D=450. Tính diện tích tứ giác có các ddirnhr là trung điểm của AB, AD, CD, BD.
Cho hình chữ nhật ABCD AB bằng 12 cm AB = 18 cm các đường phân giác của góc hình chữ nhật cắt nhau tạo thành tứ giác efgh
a,c/m efgh là hình vương
b, tính diện tích efgh
Cho tam giác ABC vuông tại A, điểm H di chuyển trên BC. Gọi E, F lần lượt là điểm đối xứng của H qua AB, AC.
a) Chứng minh tứ giác BEFC là hình thang
b) Có thể tìm được vị trí của H để BEFC trở thành hình thang vuông, hình bình hành, hình chữ nhật ko?
c) Xác định vị trí của H để tam giác EHF có diện tích lớn nhất
Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD = 3cm.
a) Tính diện tích hình bình hành ABCD
b) Gọi M là trung điểm của AB. Tính diện tích tam giác ADM
c) DM cắt AC tại N. Chứng minh DN = 2NM
d) Tính diện tích tam giác AMN