Thực hiện các phép đo cần thiết (chính xác đến mm) để tính diện tích hình ABCDE (h.152) ?
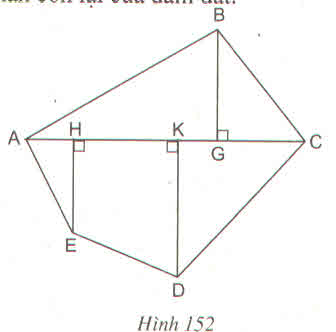
Thực hiện các phép đo cần thiết (chính xác đến mm) để tính diện tích hình ABCDE (h.152) ?

Một con đường cắt một đám đất hình chữ nhật với các dữ kiện được cho nên hình 153. Hãy tính diện tích phần con đường EBGF (EF // BG) và diện tích phần còn lại của đám đất ?
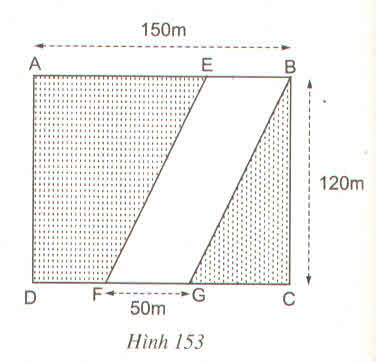
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S = SABCD - SEBGF = 18000 - 6000 = 12000(m2)
Đáp số: 6000 m2 và 12000 m2
Thực hiện các phép vẽ và đo cần thiết để tính diện tích một đám đất có dạng như hình 154, trong đó AB // CE và được vẽ với tỉ lệ \(\dfrac{1}{5000}\)
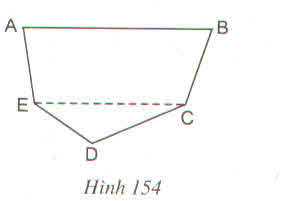
Chia đám đất ABCDE thành hình thang ABCE và tam giác ECD. Cần vẽ đường cao CH của hình thang và đường cao DK của tam giác. Thực hiện các phép đo chính xác đến mm ta được AB = 30mm, CE = 26mm, CH = 13mm, DK = 7mm.
Nên SABCE = \(\dfrac{\text{(AB+EC).CH}}{2}\) = \(\dfrac{\text{(30+26).13 }}{2}\)=364 (mm2)
SECD = \(\dfrac{1}{2}\) EC. DK = \(\dfrac{1}{2}\)267= 91 (mm2)
Do đó SABCDE = SABCE + SECD = 364 + 91 = 455 (mm2)
Vì bản đồ được vẽ với tỉ lệ xích \(\dfrac{1}{5000}\) nên diện tích đám đất là:
S = 455. 5000 = 2275000 (mm2) = 2,275 (m2)
Tính diện tích thực của một hồ nước có sơ đồ là phần gạch sọc trên hình 155 (cạnh của mỗi ô vuông là 1cm, tỉ lệ \(\dfrac{1}{10000}\)

Thực hiện các phép vẽ và đo cần thiết để tính diện tích đa giác ABCDE (BE // CD) (h.189) ?
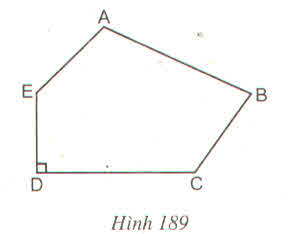
(Hình ảnh chỉ mang tính chất minh họa )
Giải:
Chia thành tam giác AEB và tứ giác EDCB
kẽ AH\(\perp EB\left(H\in EB\right)\)
Ta đo được: ED=1,5 (cm) , EB=4(cm) , CD=3(cm) , AH= 1,2(cm)
SAEB=\(\dfrac{AH.EB}{2}=\dfrac{1,2.4}{2}=2,4\left(cm^2\right)\)
SEBCD=\(\dfrac{\left(EB+DC\right).ED}{2}=\dfrac{\left(4+3\right).1,5}{2}=5,25\left(cm^2\right)\)
=> SABCDE= SAEB+SEBCD=2,4 + 5,25=7,65(cm2)
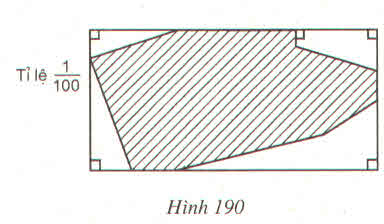
Trả lời bởi CheewinTheo bản đồ và tỉ lệ ghi trên hình 190, hãy tính diện tích của hồ nước (phần gạch sọc) ?
Theo kích thước đã cho trên hình 191, hãy tính diện tích hình gạch sọc (đơn vị là \(m^2\)) ?
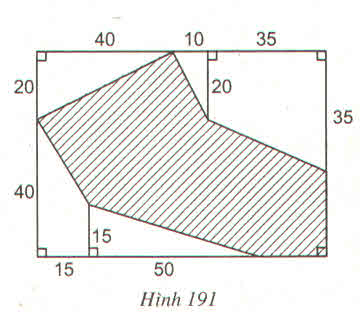
Độ dài chiều rộng của hình chữ nhật ABCD là:
20 + 40 = 60 (m)
Độ dài chiều dài của hình chữ nhật ABCD là:
40 + 10 + 35 = 85 (m)
Diện tích hình chữ nhật ABCD là:
60 . 85 = 5100 (m2).
Diện tích tam giác vuông HEN là:
\(\dfrac{10.20}{2}\)= \(\dfrac{200}{2}=100\left(m^2\right)\)
Diện tích tam giác vuông AHG là:
\(\dfrac{20.40}{2}=\dfrac{800}{2}=400\left(m^2\right)\)
Diện tích tam giác vuông MLP là:
\(\dfrac{15.50}{2}=\dfrac{750}{2}=375\left(m^2\right)\)
Diện tích hình thang vuông EBNF là:
\(\dfrac{\left(20+35\right).35}{2}=\dfrac{1925}{2}=962,5\left(m^2\right)\)
Diện tích hình thang vuông GMCL là:
\(\dfrac{\left(40+15\right).15}{2}=\dfrac{825}{2}=412,5\left(m^2\right)\)
Tổng diện tích các hình nằm ngoài hình gạch sọc và nằm trong hình chữ nhật ABCD là:
100 + 400 + 375 + 962,5 + 412,5 = 2250 (m2).
Diện tích hình sọc dọc là:
5100 - 2250 = 2850 (m2).
Vậy diện tích hình sọc dọc là 2850m2.
Trả lời bởi Dương NguyễnTìm diện tích mảnh đất theo kích thước cho trên hình 192 (đơn vị là \(m^2\) ) ?
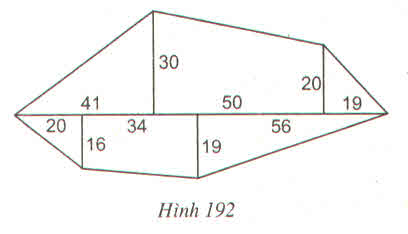

S1=\(\dfrac{30.41}{2}=615\left(cm^2\right)\)
S2=\(\dfrac{\left(30+20\right).50}{2}=1250\left(cm^2\right)\)
S3=\(\dfrac{19.20}{2}=190\left(cm^2\right)\)
S4=\(\dfrac{19.56}{2}=532\left(cm^2\right)\)
S5=\(\dfrac{\left(19+16\right).34}{2}=595\left(cm^2\right)\)
S6=\(\dfrac{16.20}{2}=160\left(cm^2\right)\)
=> S= S1 + S2 +S3 +S4 +S5 +S6= 615+1250+190+532+595+160=3342(m2)
Trả lời bởi CheewinTính diện tích của hình được cho trong mỗi trường hợp sau đây :
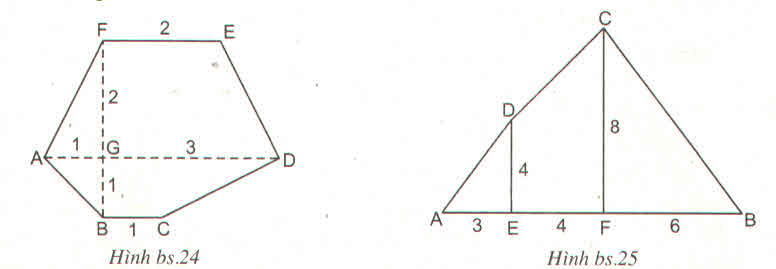
a) Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs.24
b) Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs.25)
Biết AB = 13 cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD
Bài giải:
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)
Trả lời bởi CheewinCho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính thep a, b cad S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho ?
Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên SABC = \(\dfrac{1}{2}\).BG. AC = \(\dfrac{1}{2}\) 19.48 = 456 (mm2)
SAHE = 1212 AH. HE =\(\dfrac{1}{2}\)8.16 = 64 (mm2)
SDKC = \(\dfrac{1}{2}\) KC.KD = \(\dfrac{1}{2}\)22.23 = 253(mm2)
SHKDE = (HE+KD).HK2(HE+KD).HK2 = (16+23).182(16+23).182= 351 (mm2)
Do đó
SABCDE = SABC + SAHE + SDKC + SHKDE = 456 + 64 + 253+ 351
Vậy SABCDE = 1124(mm2)
Trả lời bởi Phạm Tú Uyên