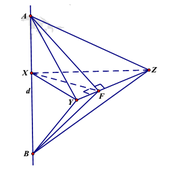
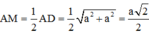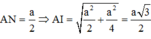Cho mặt phẳng (P) và (Q) vuông góc với nhau theo giao tuyến ∆. Trên đường thẳng ∆ lấy hai điểm A, B với AB = a. Trong mặt phẳng (P) lấy điểm C và trong mặt phẳng (Q) lấy điểm D sao cho AC, BD cũng vuông góc với ∆ và AC = BD = AB. Bán kính mặt cầu ngoại tiếp tứ diện ABCD là :
A. a 3 3
B. 2 a 3 3
C. a 3
D. a 3 2
Đáp án D

Phương pháp : Áp dụng phương pháp xác định tâm mặt cầu ngoại tiếp chóp.
Cách giải : Ta có :
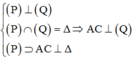
Gọi I là trung điểm của AD, do ∆ABD vuông tại nên M là tâm đường tròn ngoại tiếp ∆ABD.
Gọi N là trung điểm của AC.
Qua M kẻ đường thẳng d song song với AC => d ⊥ (ABD)
Qua N kẻ đường thẳng d’ song song với AD => d’ ⊥ AC
Gọi I = d ∩ d' => là tâm mặt cầu ngoại tiếp tứ diện ABCD có bán kính R = IA
Ta có: