Các câu hỏi tương tự
Trong không gian Oxyz cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
2
)
2...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4 và mặt phẳng (P): x-y+2z-1=0 Gọi M là một điểm bất kì trên mặt cầu (S) Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng
![]()
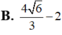
![]()
![]()
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4 và mặt phẳng (P): x-y+2z-1=0. Gọi M là một điểm bất kì trên mặt cầu (S). Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng
A. 4 6 3 - 2
B. 0
C. 6 - 2
D. 2 6 - 2
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
(
y
-
3
)
2
+
(
y
+
4
)
2
4
. Xét hai điểm M,N di động trên (S) sao cho MN1 Giá trị nhỏ nhất của
O
M...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + ( y - 3 ) 2 + ( y + 4 ) 2 = 4 . Xét hai điểm M,N di động trên (S) sao cho MN=1 Giá trị nhỏ nhất của O M 2 - O N 2 bằng
A. -10
B. - 4 - 3 5
C. -5
D. - 6 - 2 5
Trong không gian tọa độ Oxyz, cho A(-3;3;-3) thuộc mặt phẳng
(
α
)
có phương trình 2x - 2y + z + 15 0 và mặt cầu (S):
(
x
-
2
)
2
+
(
y
-
3
)
2
+
(
z
-
5
)
2...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho A(-3;3;-3) thuộc mặt phẳng ( α ) có phương trình 2x - 2y + z + 15 = 0 và mặt cầu (S): ( x - 2 ) 2 + ( y - 3 ) 2 + ( z - 5 ) 2 = 100 . Đường thẳng qua ∆ , nằm trên mặt phẳng ( α ) cắt (S) tại M, N. Để độ dài MN lớn nhất thì phương trình đường thẳng ∆ là
A. x + 3 1 = y - 3 4 = z + 3 6
B. x + 3 16 = y - 3 11 = z + 3 - 10
C. x = - 3 + 5 t y = 3 z = - 3 + 8 t
D. x - 1 3 = y - 3 - 1 = z + 3 3
Cho điểm
A
1
;
0
;
0
và mặt phẳng
P
:
y
+
z
-
3
0
. Điểm M di động trên (P), xác định độ dài ngắn nhất của AM.
Đọc tiếp
Cho điểm A 1 ; 0 ; 0 và mặt phẳng P : y + z - 3 = 0 . Điểm M di động trên (P), xác định độ dài ngắn nhất của AM.
![]()
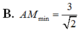
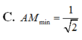
![]()
Trong không gian Oxyz, cho hai mặt cầu (S) và (S’) có tâm lần lượt là I(-1;2;3), I’(3;-2;1) và có bán kính lần lượt là 4 và 2. Cho điểm M di động trên mặt cầu (S), N di động trên mặt cầu (S’). Khi đó giá trị lớn nhất của đoạn thẳng MN bằng: A. 8 B. 2 C. 12 D. 6
Đọc tiếp
Trong không gian Oxyz, cho hai mặt cầu (S) và (S’) có tâm lần lượt là I(-1;2;3), I’(3;-2;1) và có bán kính lần lượt là 4 và 2. Cho điểm M di động trên mặt cầu (S), N di động trên mặt cầu (S’). Khi đó giá trị lớn nhất của đoạn thẳng MN bằng:
A. 8
B. 2
C. 12
D. 6
Trong không gian Oxyz, cho hai điểm A(-14;13;-4), B(-7;-1;1). Xét điểm M di động trên mặt cầu (S):
(
x
+
5
)
2
+
(
y
+
5
)
2
+
(
z
-
14
)...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(-14;13;-4), B(-7;-1;1). Xét điểm M di động trên mặt cầu (S): ( x + 5 ) 2 + ( y + 5 ) 2 + ( z - 14 ) 2 = 324 Giá trị lớn nhất của 2MA – 3MB bằng
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S):
x
-
1
2
+
y
-
1
2
+
z
-
1
2
12
và mặt phẳng (P): x-2y+2z+110. Xét điểm M di động trên (P); các điểm A, B...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y - 1 2 + z - 1 2 = 12 và mặt phẳng (P): x-2y+2z+11=0. Xét điểm M di động trên (P); các điểm A, B, C phân biệt di động trên (S) sao cho AM, BM, CM là các tiếp tuyến của (S). Mặt phẳng (ABC) luôn đi qua điểm cố định nào dưới đây?
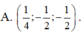
![]()
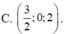
![]()
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
−
4
x
+
2
y
−
6
z
+
5
0
và mặt phẳng
P
:
2
x
+
2
y
−
z
+
16
0...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 4 x + 2 y − 6 z + 5 = 0 và mặt phẳng P : 2 x + 2 y − z + 16 = 0 . Điểm M, N di động lần lượt trên (S) và (P). Khi đó giá trị nhỏ nhất của đoạn MN là
A. 8
B. 3
C. 2
D. 5


