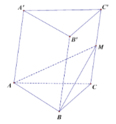
Hình chóp MABC có cùng diện tích đáy với hình lăng trụ
Và có chiều cao bằng 2 lăng trụ nên
V 2 = 1 6 V ABC . A ' B ' C ' ⇒ V 1 = 5 6 V ABC . A ' B ' C ' ⇒ V 1 V 2 = 5
Đáp án cần chọn là C
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Hình chóp MABC có cùng diện tích đáy với hình lăng trụ
Và có chiều cao bằng 2 lăng trụ nên
V 2 = 1 6 V ABC . A ' B ' C ' ⇒ V 1 = 5 6 V ABC . A ' B ' C ' ⇒ V 1 V 2 = 5
Đáp án cần chọn là C
Cho lăng trụ tam giác A B C . A ' B ' C ' . Mặt phẳng đi qua A, B và trung điểm M của cạnh C C ' chia lăng trụ thành 2 phần có thể tích V 1 , V 2 V 1 > V 2 . Tỉ số V 1 V 2 là
A. 4
B. 2
C. 5
D. 3
Cho lăng trụ tam giác ABC.A′B′C′. Gọi M,N,P lần lượt là trung điểm các cạnh A′B′,BC,CC′. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần, phần chưa điểm B có thể tích là V 1 . Gọi V là thể tích khối lăng trụ. Tính V 1 V .
A. 25 288
B. 29 144
C. 37 288
D. 19 144
Cho hình lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh 3 . Gọi I là trung điểm của cạnh BC. Biết thể tích lăng trụ là V=6 , khoảng cách từ I đến mặt phẳng (A'B'C') là:
A. 8 3
B. 8 3 3
C. 4 3
D. 4 3 3
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có góc giữa hai mặt phẳng A ' B C và A B C bằng 60 ° , cạnh A B = a . Tính thể tích V của khối lăng trụ A B C . A ' B ' C ' ?
A. V = a 3 3 4 .
B. V = 3 a 3 4 .
C. V = 3 a 3 3 8 .
D. V = a 3 3 .
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60 0 , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A′B′C′ là
A. 3 3 4
B. 3
C. 3
D. 3 3
Cho lăng trụ ABC.A’B’C’ có thể tích V, gọi M, N, P lần lượt thuộc cạnh AA’; BB’; CC’ sao cho 2 M A = M A ' , N B = N B ' ; 3 P C = P C ' . Mặt phẳng chia khối lăng trụ A B C . A ' B ' C ' thành hai phần. Tính tỉ số thể tích hai phần này (số bé chia số lớn).
A. 17 19
B. 17 36
C. 13 23
D. 13 36
Cho lăng trụ A B C . A ' B ' C ' có đáy là tam giác vuông tại . Biết góc giữa mặt phẳng A ' B C và mặt phẳng (ABC) bằng 60 0 và hình chiếu vuông góc của A’ trên (ABC) là trung điểm H của AB. Tính thể tích V của khối lăng trụ đó.
A. V = a 3 6
B. V = a 3 2
C. V = a 3 6 2
D. V = a 3 2 2
Cho khối lăng trụ ABC.A′B′C′ có thể tích V, đáy là tam giác cân, AB = AC. Gọi E là trung điểm cạnh AB và F là hình chiếu vuông góc của E lên BC. Mặt phẳng (C′EF) chia khối lăng trụ đã cho thành hai khối đa diện. Tính thể tích của khối đa diện chứa đỉnh A.
A. 47 72 V
B. 25 72 V
C. 29 72 V
D. 43 72 V
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB',CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B , V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2