Các câu hỏi tương tự
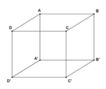
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông cân tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB 3a, AA’ 6a. A.
V
7
a
3
.
B.
V
6
2
a
3
.
C.
V
8
a...
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông cân tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
A. V = 7 a 3 .
B. V = 6 2 a 3 .
C. V = 8 a 3 .
D. V = 6 a 3 .
Cho lăng trụ đứng tam giác
A
B
C
.
A
B
C
có đáy ABC là tam giác vuông cân tại B với
B
A
B
C
a
,
biết măṭ phẳng ( A’BC) hợp với măṭ phẳng đáy ( ABC) một góc
60
°
.
Tính thể tích khối lăng trụ đã cho. A.
3
a
3...
Đọc tiếp
Cho lăng trụ đứng tam giác A B C . A ' B ' C ' có đáy ABC là tam giác vuông cân tại B với B A = B C = a , biết măṭ phẳng ( A’BC) hợp với măṭ phẳng đáy ( ABC) một góc 60 ° . Tính thể tích khối lăng trụ đã cho.
A. 3 a 3
B. a 3 2
C. 2 3 a 3 3
D. a 3 3 2
Cho hình trụ có hai đường tròn đáy lần lượt là (O); (O’). Biết thể tích khối nón có đỉnh là O và đáy là hình tròn (O’) là
a
3
, tính thể tích khối trụ đã cho ? A. 2
a
3
B. 4
a
3
C. 6
a
3
D. 3
a
3
Đọc tiếp
Cho hình trụ có hai đường tròn đáy lần lượt là (O); (O’). Biết thể tích khối nón có đỉnh là O và đáy là hình tròn (O’) là a 3 , tính thể tích khối trụ đã cho ?
A. 2 a 3
B. 4 a 3
C. 6 a 3
D. 3 a 3
Cho hı̀nh chóp S.ABCD có SA vuông góc với mặt phẳng
A
B
C
D
, đáy là hình thang ABCD vuông tại A và B có
A
B
a
,
A
D
3
a
,
B
C
a
. Biết
S
A
a
3
, tính thể tích khối chóp S.BCD theo...
Đọc tiếp
Cho hı̀nh chóp S.ABCD có SA vuông góc với mặt phẳng A B C D , đáy là hình thang ABCD vuông tại A và B có A B = a , A D = 3 a , B C = a . Biết S A = a 3 , tính thể tích khối chóp S.BCD theo a
A. 2 3 a 3
B. 3 a 3 6
C. 2 3 a 3 3
D. 3 a 3 4
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc
B
A
D
^
60
°
,
AB’ hợp với đáy (ABCD) một góc
30
°
.
Thể tích khối hộp là: A.
a
3
2
B.
a
3...
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc B A D ^ = 60 ° , AB’ hợp với đáy (ABCD) một góc 30 ° . Thể tích khối hộp là:
A. a 3 2
B. a 3 6
C. 3 a 3 2
D. a 3 3 6
Cho hình chóp S.ABC có đáy ABCD là tam giác vuông tại C, AB
5
a,ACa. Cạnh SA3a và vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng A.
a
3
B.
5
2
a
3
C.
2
a
3
D.
3
a
3
Đọc tiếp
Cho hình chóp S.ABC có đáy ABCD là tam giác vuông tại C, AB= 5 a,AC=a. Cạnh SA=3a và vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng
A. a 3
B. 5 2 a 3
C. 2 a 3
D. 3 a 3
Cho lăng trụ đứng ABC.A’B’C’ có AB AC a,
B
C
a
3
. Cạnh bên AA 2a. Bán kính mặt cầu ngoại tiếp tứ diện AB’C’C bằng A. a B.
a
5
C.
a
3
D.
a
2
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’ có AB = AC = a, B C = a 3 . Cạnh bên AA' = 2a. Bán kính mặt cầu ngoại tiếp tứ diện AB’C’C bằng
A. a
B. a 5
C. a 3
D. a 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
2
2
, cạnh bên SA vuông góc với mặt phẳng đáy và SA3 Mặt phẳng
α
qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP. A.
V
64
2
π
3
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA=3 Mặt phẳng α qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
A. V = 64 2 π 3
B. V = 125 π 6
C. V = 32 π 3
D. V = 10 Sπ 3
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SA và CD bằng
3
a. Thể tích khối chóp S.ABCD bằng A.
a
3
3
3
B.
4
a
3
3
C.
a
3
3
D. ...
Đọc tiếp
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SA và CD bằng 3 a. Thể tích khối chóp S.ABCD bằng
A. a 3 3 3
B. 4 a 3 3
C. a 3 3
D. a 3 4 3 3