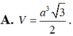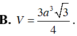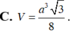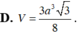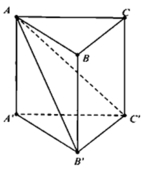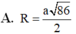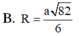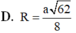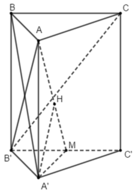
+ Gọi M là trung điểm của B’C’
Tam giác AB’C’ cân tại A ⇒ AM ⊥ B’C’
Tam giác A’B’C’ cân tại A’ ⇒ A’M ⊥ B’C’
Mà (AB’C’) ∩ (A’B’C’) = B’C’
Do đó góc giữa hai mặt phẳng (AB’C’) và (A’B’C’) là góc giữa 2 đường thẳng AM và A’M và chính là góc AMA’ ⇒ A M A ' ^ = 60 °
Ta có: A’M = 1/2 A’C’ = a/2 ⇒ AA’ = A’M. tan 60 ° = a 3 2
+ Ta có BC // (AB’C’) ⇒ d(BC; (AB’C’)) = d(B; (AB’C’))
Ta chứng minh được d(B; (AB’C’)) = d(A’; (AB’C’))
Do đó: d(BC; (AB’C’)) = d(A’; (AB’C’))
+ Ta chứng minh được (AA’M) ⊥ (AB’C’), trong mặt phẳng (AA’M), dựng A’H ⊥ AM tại H
⇒ A’H ⊥ (AB’C’) ⇒ d(A’; (AB’C’)) = A’H ⇒ d(BC; (AB’C’)) = A’H
+ Tính A’H
Ta có: 1 A ' H 2 = 1 A A ' 2 + 1 A ' M 2 ⇒ A’H = a 3 4
Vậy d(BC; (AB’C’)) = a 3 4 .
Đáp án B