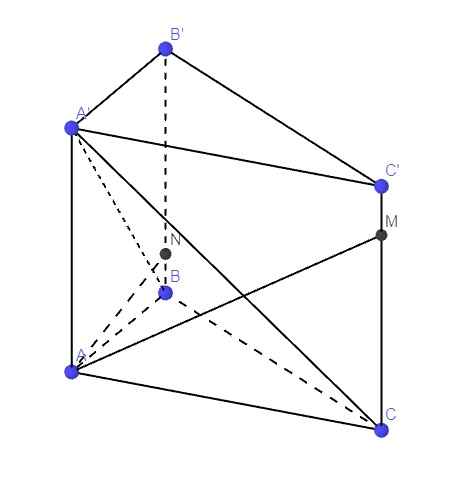
a.
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)