Các câu hỏi tương tự
Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Các điểm M, N, P lần lượt thuộc các cạnh AA’, BB’, CC’ sao cho
A
M
A
A
1
2
,
B
N
B
B
C
P...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Các điểm M, N, P lần lượt thuộc các cạnh AA’, BB’, CC’ sao cho A M A A ' = 1 2 , B N B B ' = C P C C ' = 2 3 . Thể tích khối đa diện ABC.MNP bằng:
A. 2 3 V
B. 9 16 V
C. 20 27 V
D. 11 18 V
Cho hình lăng trụ đều ABC.A’B’C có AB2a, AA3a Gọi M, N, P lần lượt là trung điểm của AA’, A’C, AC. Tính theo a thể tích V của khối tứ diện B.MNP.
Đọc tiếp
Cho hình lăng trụ đều ABC.A’B’C có AB=2a, AA'=3a Gọi M, N, P lần lượt là trung điểm của AA’, A’C, AC. Tính theo a thể tích V của khối tứ diện B.MNP.
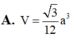
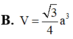
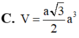
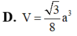
Cho hình lăng trụ ABC.A’B’C’, trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA 4AM, BB 4BN. Mặt phẳng (CMN) chia khối lăng trụ thành hai phần. Gọi
V
1
là thể tích khối chóp C’.A’B’MN và
V
2
là thể tích khối đa diện ABCMNC’. Tính tỷ số
V
1
V
2
A.
V...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’, trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA' = 4A'M, BB' = 4B'N. Mặt phẳng (C'MN) chia khối lăng trụ thành hai phần. Gọi V 1 là thể tích khối chóp C’.A’B’MN và V 2 là thể tích khối đa diện ABCMNC’. Tính tỷ số V 1 V 2
A. V 1 V 2 = 1 5
B. V 1 V 2 = 4 5
C. V 1 V 2 = 2 5
D. V 1 V 2 = 3 5
Cho hình lăng trụ ABC.A’B’C’có thể tích bằng V. Gọi M, N lần lượt là trung điểm của A’B’, AC và P là điểm thuộc cạnh CC’ sao cho CP 2C’P (như hình vẽ). Tính thể tích khối tứ diện BMNP theo V.
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’có thể tích bằng V. Gọi M, N lần lượt là trung điểm của A’B’, AC và P là điểm thuộc cạnh CC’ sao cho CP = 2C’P (như hình vẽ). Tính thể tích khối tứ diện BMNP theo V.
![]()
![]()
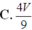
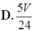
Cho hình lăng trụ ABC.ABC có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC’, BB’. Thể tích của khối tứ diện CMNP bằng
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A'C’, BB’. Thể tích của khối tứ diện CMNP bằng
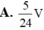
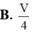
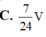
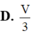
Cho khối lăng trụ đứng ABC.A’B’C’ có BB’ a, đáy ABC là tam giác vuông cân tại B, AB a. Tính thể tích V của khối lăng trụ.
Đọc tiếp
Cho khối lăng trụ đứng ABC.A’B’C’ có BB’ = a, đáy ABC là tam giác vuông cân tại B, AB = a. Tính thể tích V của khối lăng trụ.


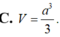
![]()
Cho hình lăng trụ đứng ABC.A’B’C’ có AB1,AC2,AA3 và BAC
120
o
Gọi M, N lần lượt là các điểm trên cạnh BB’, CC’ sao cho BM3BM;CN2CN Tính khoảng cách từ điểm M đến mặt phẳng (ABN)
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có AB=1,AC=2,AA'=3 và BAC= 120 o Gọi M, N lần lượt là các điểm trên cạnh BB’, CC’ sao cho BM=3B'M;CN=2C'N Tính khoảng cách từ điểm M đến mặt phẳng (A'BN)

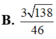
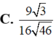
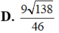
Cho khối lăng trụ tam giác ABC.ABC có thể tích là V. Gọi I, J lần lượt là trung điểm của hai cạnh AA và BB. Khi đó thể tích của khối đa diện ABCIJC bằng
Đọc tiếp
Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích là V. Gọi I, J lần lượt là trung điểm của hai cạnh AA' và BB'. Khi đó thể tích của khối đa diện ABCIJC' bằng

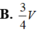
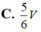
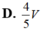
Cho lăng trụ tam giác ABC.A’B’C’ có thể tích là V. Gọi M, N là trung điểm của AB và CC'. Thể tích khối tứ diện B’MCN tính theo V là:
A. V 2
B. V 4
C. V 3
D. V 12