Các câu hỏi tương tự
Cho khối nón có bán kính đáy r
3
và chiều cao gấp 2 lần bán kính đáy. Tính thể tích khối nón đã cho
A
.
6
3
π
B
.
2
3
π
C
.
2
π
D
.
6
π
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao gấp 2 lần bán kính đáy. Tính thể tích khối nón đã cho
A . 6 3 π
B . 2 3 π
C . 2 π
D . 6 π
Cho khối nón có bán kính đáy r
3
và chiều cao h4 Tính thể tích V của khối nón đã cho.
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao h=4 Tính thể tích V của khối nón đã cho.
![]()
![]()
![]()
![]()
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N).
S
x
q
,
S
t
p
,
V
lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A
.
V
1...
Đọc tiếp
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N). S x q , S t p , V lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A . V = 1 3 πrh
B . l 2 = h 2 + r 2
C . S t p = πr ( 1 + r )
D . S x q = πrl
Cho khối nón có bán kính đáy r
3
và chiều cao h4 Tính thể tích V của khối nón đã cho.
Đọc tiếp
Cho khối nón có bán kính đáy r= 3 và chiều cao h=4 Tính thể tích V của khối nón đã cho.
![]()
![]()
![]()
![]()
Hình nón tròn xoay có chiều cao h=3a bán kính đường tròn đáy r=3 Thể tích khối nón bằng
![]()
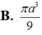
![]()
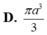
Cho hình nón (N) có đường cao SO h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM x, 0 x h. (C ) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất A.
h
2
B.
h
2
2
C.
h
3...
Đọc tiếp
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM = x, 0 < x <h. (C ) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất
A. h 2
B. h 2 2
C. h 3 2
D. h 3
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kỳ nội tiếp mặt cầu (S) Thể tích khối nón (H) là
V
1
thể tích phần còn lại của khối cầu là
V
2
Giá trị lớn nhất của
V
1
V
2
bằng: A.
81
32
B.
76
32...
Đọc tiếp
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kỳ nội tiếp mặt cầu (S) Thể tích khối nón (H) là V 1 thể tích phần còn lại của khối cầu là V 2 Giá trị lớn nhất của V 1 V 2 bằng:
A. 81 32
B. 76 32
C. 32 81
D. 32 76
Cho hình nón có chiều cao h, đường tròn đáy có bán kính R. Một mặt phẳng (P) di động song song với đáy hình nón cắt hình nón theo đường tròn giao tuyến (L) Dựng hình trụ có một đáy là đường tròn (L) một đáy nằm trên đáy hình nón có trục là trục của hình nón. Gọi x là chiều cao của hình trụ, giá trị của x để hình trụ có thể tích lớn nhất A.
x
h
2
B.
x
...
Đọc tiếp
Cho hình nón có chiều cao h, đường tròn đáy có bán kính R. Một mặt phẳng (P) di động song song với đáy hình nón cắt hình nón theo đường tròn giao tuyến (L) Dựng hình trụ có một đáy là đường tròn (L) một đáy nằm trên đáy hình nón có trục là trục của hình nón. Gọi x là chiều cao của hình trụ, giá trị của x để hình trụ có thể tích lớn nhất
A. x = h 2
B. x = h 3
C. x = h 4
D. x= h
Giá trị lớn nhất của thể tích khối nón nội tiếp trong khối cầu có bán kính R là:
A
.
1
3
πR
3
B
.
4
3
πR
3
C
.
4
2
9
πR
3
D...
Đọc tiếp
Giá trị lớn nhất của thể tích khối nón nội tiếp trong khối cầu có bán kính R là:
A . 1 3 πR 3
B . 4 3 πR 3
C . 4 2 9 πR 3
D . 32 81 πR 3


