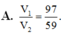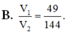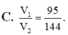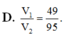Các câu hỏi tương tự
Cho khối hộp chữ nhật
A
B
C
D
.
A
B
C
D
có thể tích bằng 2110. Biết
A
M
M
A
;
D
N
3
N
D
;
C
P
2
P
C
. Mặt phẳng
M
N
P...
Đọc tiếp
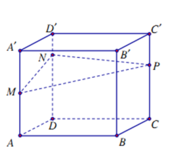
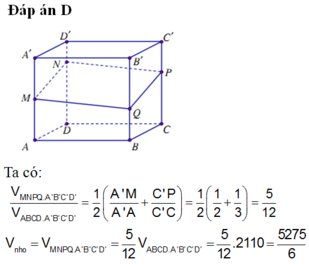
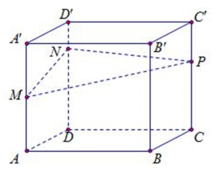
Cho khối hộp chữ nhật A B C D . A ' B ' C ' D ' có thể tích bằng 2110. Biết A ' M = M A ; D N = 3 N D ' ; C P = 2 P C ' . Mặt phẳng M N P chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng
A. 7385 18
B. 5275 12
C. 8440 9
D. 5275 6
Cho khối hộp chữ nhật ABCD.ABCD có thể tích là V. Biết AM MA, DN 3ND, CP 2PC. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Tính thể tích khối đa diện nhỏ hơn tính theo V bằng? A.
5
V
12
B.
7
V
12
C.
V
4
D.
V
6
Đọc tiếp
Cho khối hộp chữ nhật ABCD.A'B'C'D' có thể tích là V. Biết A'M = MA, DN = 3ND', CP = 2PC'. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Tính thể tích khối đa diện nhỏ hơn tính theo V bằng?
A. 5 V 12
B. 7 V 12
C. V 4
D. V 6
Cho khối hộp chữ nhật ABCD. ABCD có thể tích bằng 2110. Biết (MNP), DN3ND, CP2CP như hình vẽ. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng: A.
5275
6
B.
8440
9
C.
7485
18
D.
5275
12
Đọc tiếp
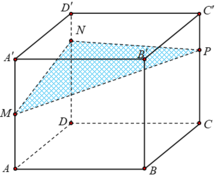
Cho khối hộp chữ nhật ABCD. A'B'C'D' có thể tích bằng 2110. Biết (MNP), DN=3ND', CP=2C'P như hình vẽ. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng:
A. 5275 6
B. 8440 9
C. 7485 18
D. 5275 12
Cho khối hộp ABCD.ABCD có thể tích bằng 2018. Gọi M là trung điểm của cạnh AB. Mặt phẳng (MBD) chia khối chóp ABCD.ABCD thành hai khối đa diện. Tính thể tích phần khối đa diện chứa đỉnh A A.
5045
6
B.
7063
6
C.
10090
17
D.
7063
12
Đọc tiếp
Cho khối hộp ABCD.A'B'C'D' có thể tích bằng 2018. Gọi M là trung điểm của cạnh AB. Mặt phẳng (MB'D') chia khối chóp ABCD.A'B'C'D' thành hai khối đa diện. Tính thể tích phần khối đa diện chứa đỉnh A
A. 5045 6
B. 7063 6
C. 10090 17
D. 7063 12
Cho khối hộp ABCD.ABCD, điểm M nằm trên cạnh CC’ thỏa mãn CC’ 3CM. Mặt phẳng (AB’M) chia khối hộp thành hai khối đa diện. Gọi V1 là thể tích khối đa diện chứa đỉnh A’,V2 là thể tích khối đa diện chứa đỉnh B. Tính tỉ số thể tích V1 và V2. A.
1
27
B.
27
7
C.
7
20
D.
9
4
Đọc tiếp
Cho khối hộp ABCD.A'B'C'D', điểm M nằm trên cạnh CC’ thỏa mãn CC’ = 3CM. Mặt phẳng (AB’M) chia khối hộp thành hai khối đa diện. Gọi V1 là thể tích khối đa diện chứa đỉnh A’,V2 là thể tích khối đa diện chứa đỉnh B. Tính tỉ số thể tích V1 và V2.
A. 1 27
B. 27 7
C. 7 20
D. 9 4
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh
A
B
và sao cho
M
A
M
B
và
N
B
2
N
C
. Mặt phẳng
D
M...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh A ' B ' và sao cho M A ' = M B ' và N B = 2 N C . Mặt phẳng D M N chia khối lập phương đã cho thành hai khối đa diện. Gọi V H là thể tích khối đa diện chứa đỉnh A , V H ' là thể tích khối đa diện còn lại. Tỉ số V H V H ' bằng
A. 151 209
B. 209 360
C. 2348 3277
D. 151 360
Cho khối lập phương ABCD.ABCD cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MBDN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:A.
a
3
9
B.
a
3
6
C.
a...
Đọc tiếp
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho BE = EB′/2, DF = FD′/2. Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B, kéo dài lấy điểm M sao cho BM
1
2
AB. Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứa đỉnh A’ có thể tích
V
1
và khối đa diện chứa đỉnh C’ có thể tích
V
2
. Tính
V
1...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B, kéo dài lấy điểm M sao cho B'M= 1 2 A'B'. Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứa đỉnh A’ có thể tích V 1 và khối đa diện chứa đỉnh C’ có thể tích V 2 . Tính V 1 V 2 .