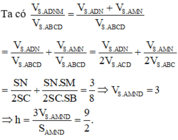Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
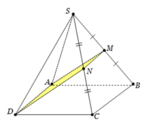
Cho khối chóp S.ABCD có thể tích bằng 8. Gọi M, N lần lượt là trung điểm của SB, SC và ABCD là hình bình hành (như hình vẽ).Biết diện tích của tứ giác AMND bằng 2. Tính khoảng cách h từ đỉnh S tới mặt phẳng (AMND). A.
h
3
2
B.
h
8
3
C.
h
3
D.
h
9...
Đọc tiếp
Cho khối chóp S.ABCD có thể tích bằng 8. Gọi M, N lần lượt là trung điểm của SB, SC và ABCD là hình bình hành (như hình vẽ).
Biết diện tích của tứ giác AMND bằng 2. Tính khoảng cách h từ đỉnh S tới mặt phẳng (AMND).
A. h = 3 2
B. h = 8 3
C. h = 3
D. h = 9 2
Cho hình chóp tứ giác
S
.
A
B
C
D
đáy là hình bình hành có thể tích bằng V. Lấy điểm B’, D’ lần lượt là trung điểm của cạnh SB và SD. Mặt phẳng qua
A
B
D
cắt cạnh SC tại C’. Khi đó thể tích khối chóp
S
.
A
B
C
D
bằng A. ...
Đọc tiếp
Cho hình chóp tứ giác S . A B C D đáy là hình bình hành có thể tích bằng V. Lấy điểm B’, D’ lần lượt là trung điểm của cạnh SB và SD. Mặt phẳng qua A B ' D ' cắt cạnh SC tại C’. Khi đó thể tích khối chóp S . A B ' C ' D ' bằng
A. V 3
B. 2 V 3
C. V 3 3
D. V 6
Cho hình chóp tứ giác S.ABCD đáy là hình bình hành có thể tích bằng V. Lấy điểm B, D lần lượt là trung điểm của các cạnh SB và SD. Mặt phẳng (ABD) cắt cạnh SC tại C. Khi đó thể tích khối chóp S.ABCD bằng A.
V
3
B.
2
V
3
C.
V
3
3
D.
V
6
Đọc tiếp
Cho hình chóp tứ giác S.ABCD đáy là hình bình hành có thể tích bằng V. Lấy điểm B', D' lần lượt là trung điểm của các cạnh SB và SD. Mặt phẳng (AB'D') cắt cạnh SC tại C'. Khi đó thể tích khối chóp S.AB'C'D' bằng
A. V 3
B. 2 V 3
C. V 3 3
D. V 6
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên
S
C
a
15
.
Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng
2
a
6
.
Tính thể tích V của khối chóp S.ABCD? A.
V
8
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên S C = a 15 . Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2 a 6 . Tính thể tích V của khối chóp S.ABCD?
A. V = 8 a 3 6 .
B. V = 12 a 3 6 .
C. V = 4 a 3 6 .
D. V = 24 a 3 6 .
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi
V
1
, V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số
V
1
V
bằng: A.
1
2
B.
2
3
C.
1...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi V 1 , V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số V 1 V bằng:
A. 1 2
B. 2 3
C. 1 3
D. 3 8
Cho hình chóp S.ABCDvới đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên
S
C
a
15
.
Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng
2
6
a
.
Tính thể tích V của khối chóp S,ABCD? A.
V
8...
Đọc tiếp
Cho hình chóp S.ABCDvới đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên S C = a 15 . Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng 2 6 a . Tính thể tích V của khối chóp S,ABCD?
A. V = 8 6 a 3
B. V = 12 6 a 3
C. V = 4 6 a 3
D. V = 24 6 a 3
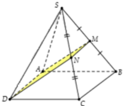
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
B
A
D
^
60
°
và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2

A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K,M lần lượt là trung điểm của các đoạn thẳng SA, SB, (α) là mặt phẳng qua K song song với AC và AM. Mặt phẳng (α) chia khối chóp S.ABCD thành hai khối đa diện. Gọi
V
1
là thể tích của khối đa diện chứa đỉnh S và
V
2
là thể tích khối đa diện còn lại. Tính tỉ số
V
1
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K,M lần lượt là trung điểm của các đoạn thẳng SA, SB, (α) là mặt phẳng qua K song song với AC và AM. Mặt phẳng (α) chia khối chóp S.ABCD thành hai khối đa diện. Gọi V 1 là thể tích của khối đa diện chứa đỉnh S và V 2 là thể tích khối đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 25
B. V 1 V 2 = 5 11
C. V 1 V 2 = 7 17
D. V 1 V 2 = 9 23
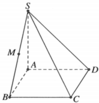
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật cạnh AB a, AD
a
2
, cạnh bên SA vuông góc với mặt phẳng (ABCD), góc giữa SC và mặt phẳng (ABCD) bằng 60 độ. Gọi M là trung điểm của cạnh SB (tham khảo hình vẽ). Khoảng cách từ điểm M tới mặt phẳng (ABCD) bằng A. a/2 B. 3a/2 C.
2
a
3
D.
a
3
Đọc tiếp
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật cạnh AB = a, AD = a 2 , cạnh bên SA vuông góc với mặt phẳng (ABCD), góc giữa SC và mặt phẳng (ABCD) bằng 60 độ. Gọi M là trung điểm của cạnh SB (tham khảo hình vẽ). Khoảng cách từ điểm M tới mặt phẳng (ABCD) bằng
A. a/2
B. 3a/2
C. 2 a 3
D. a 3