Đáp án D

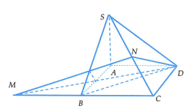
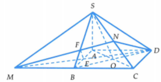
Gọi O là tâm hình vuông ABCD
G là trọng tâm tam giác đều SBC
Đường thẳng qua O vuông góc với (ABC cắt đường thẳng qua G vuông góc với (SBC) tại I
Khi đó R S . A B C D = S I = G I 2 + O H 2 = S 4 π
Đặt A D = A B = a ⇒ S G = a 3 3 ; O H = a 2
Suy ra a 2 3 + a 2 4 = 21 ⇒ a = 6
Dựng A x / / B D ; H E ⊥ A x , H F ⊥ S A E ⇒ d B D ; S A = d B ; S A x = 2 d H = 2 E F
Lại có A E = A H sin 45 ° = 3 2 2 ; S H = 3 3 ⇒ H F = S H . H E S H 2 + H E 2 = 2 21 7
Do đó d S A ; B D = 6 21 7