Chọn A
Ta có 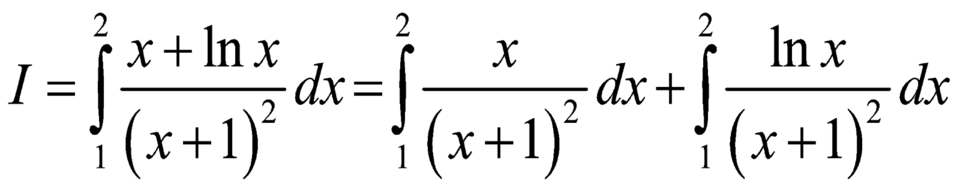 .
.
Xét 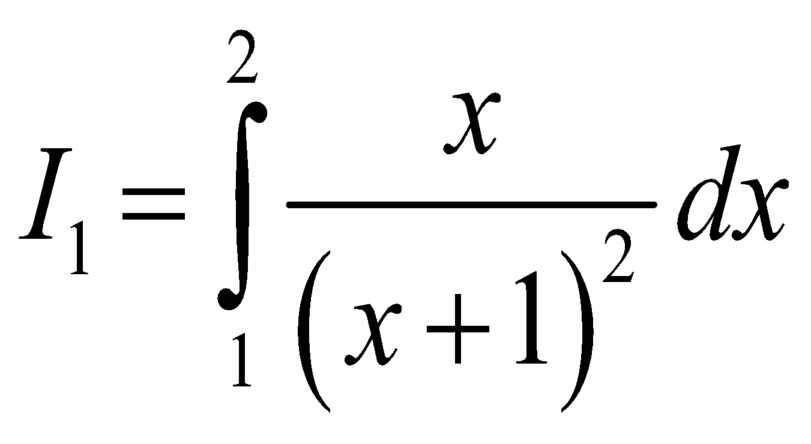 .
.
Đặt ![]() .
.
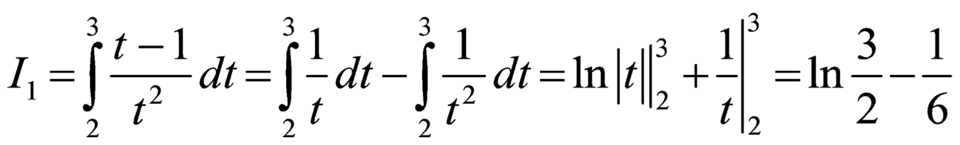 .
.
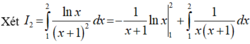
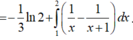
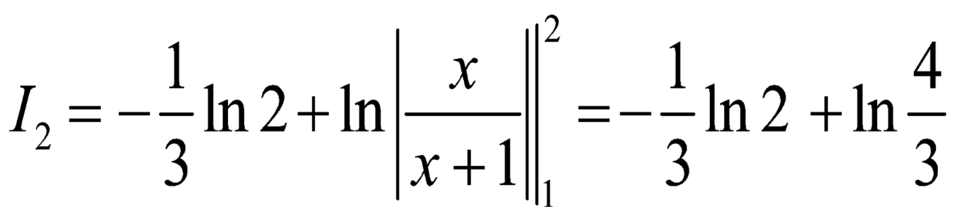 .
.
Do đó ![]() .
.
![]() .
.
Chọn A
Ta có 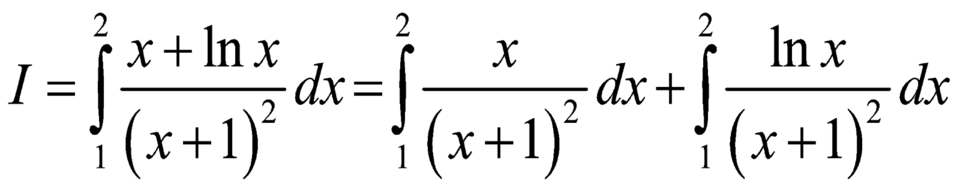 .
.
Xét 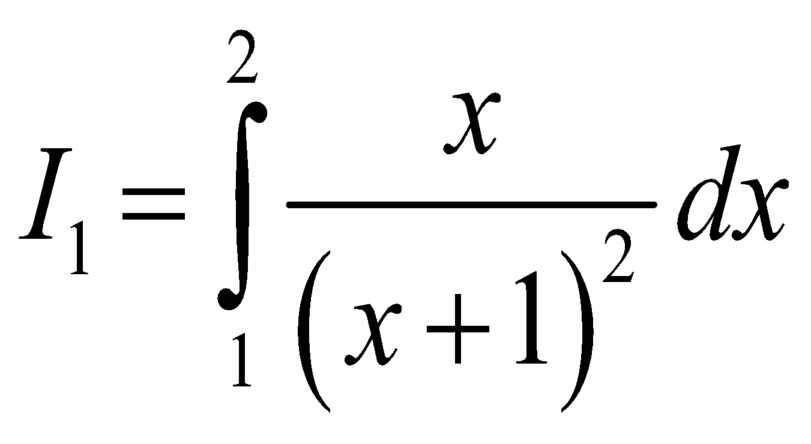 .
.
Đặt ![]() .
.
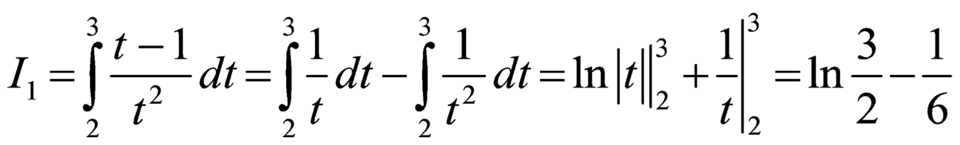 .
.
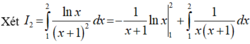
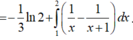
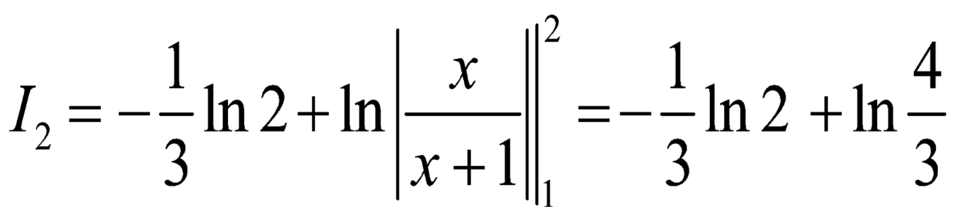 .
.
Do đó ![]() .
.
![]() .
.
Cho ∫ 1 2 ln x ( x + 1 ) 2 d x = a b ln 2 - ln c với a , b , c là các số nguyên dương và a b là phân số tối giản. Tính giá trị của biểu thức S = a + b c
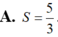
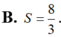
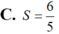

Cho ∫ 0 9 16 1 x + 1 + x = a - b ln 2 c với a,b,c là các số nguyên dương và a/b tối giản. Giá trị của biểu thức a+b+c bằng
A. 43.
B. 48.
C. 88.
D. 33.
Biết I = ∫ 0 4 x ln ( 2 x + 1 ) d x = a b ln 3 - c , trong đó a, b, c là các số nguyên dương và a/b là phân số tối giản. Tính S = a+b+c
A. S = 60
B. S = 17
C. S = 72
D. S = 68
Cho tích phân ∫ 1 2 ln x x 2 d x = b c + a ln 2 với a là số thực, b và c là các số nguyên dương, đồng thời b c là phân số tối giản. Tính giá trị của biểu thức P=2a+3b+c
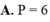

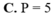
![]()
Cho biết ∫ 0 1 x 2 . e x ( x + 2 ) 2 d x = a b e + c với a,c là các số nguyên , b là số nguyên dương và a/b là phân số tối giản. Tính a-b+c
A. 3.
B. 0.
C. 2.
D. -3.
Cho tích phân I = ∫ 1 2 ln x x 2 d x = b c + a ln 2 với a là số thực, b và c là các số nguyên dương, đồng thời b c là phân số tối giản. Tính giá trị của biểu thức
P = 2a + 3b + c.
A. P=6
B. P=-6
C. P=5
D. P=4
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(x) + f( π 3 - x )= 1 2 sin x cos x ( 8 cos 3 x + 1 ) , ∀ x ∈ R Biết tích phân I= ∫ 0 π 3 f ( x ) d x được biểu diễn dưới dạng I= a b ln c d ; a , b , c , d ∈ Z và các phân số a b ; c d là các phân số tối giản. Tính S= a 3 + a b - c + d
![]()
![]()
![]()
![]()
Biết ∫ 0 1 x d x 5 x 2 + 4 = a b với a, b là các số nguyên dương và phân thức a/b là tối giản. Tính giá trị của biểu T = a 2 + b 2
A. T =13
B. T = 26
C. T = 29
D. T = 34
Cho ∫ 0 8 1 + 1 + x d x = a - b c với a,b,c là các số nguyên dương và a/c tối giản. Giá trị biểu thức a+b+c bằng
A. 111.
B. 239.
C. 255.
D. 367.