a) Có AD=BC=5a, AC=12a
Xét tam giác ABC vuộng tại C=> AB^2 =169a^2 <=> AB= 13a ( đlý Pitago )
Xét tam giác ABC vuộng tại C, có: SinABC =12a/13a, CosABC= 5a/13a
=> ( sin B + cosB )/ (sinB -cosB) = ( 12a/13a + 5a/13a)/(12a/13a - 5a/13a)= 17/7
b) Trong tam giác ADC, Kẻ AH vuông góc DC
Trong tam giác ACB, Kẻ CK vuông góc AB
Có AB//DC ( t/c hình thang)
mà AD vuông góc DC
=> AD vuông góc AB (1)
Tương tự có CK vuông góc DC (2)
(1)(2) => tứ giác ABCD là hcn ( dhnb hcn)
=> AD=CK
Xét tam giác ABC vuông tại C có CK là đường cao AB
<=> AB.CK= CB.CA
=> 13a.CK = 5a.12a
<=> CK= (60/13)a = AH
Xét tam giác AHC vuông tại H có HC= (144/13)a ( pitago)
Xét tam giác AHD vuông tại H có HD= (25/13)a ( pitago)
Mà H nằm giữa DC => DC = HC + HD = 13a
=> S ABCD= 1/2AH(AB+CD)= 1/2. (60/13)a. (13a +13a)= 60 a^2 (đvdt)
Chúc bạn học tốt!!!!!!
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD 5a, AC 12aTính sin
sin
B
+
c
o
s
B
sin
B
-
cos
B
Đọc tiếp
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a
Tính sin sin B + c o s B sin B - cos B
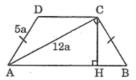
Cho hình thang ABCD có cạnh bên AD và bc bằng nhau, đg chéo AC vuông góc với cạnh bên BC biết AD=5a, AC=12a. Tính
\(a.\frac{sinB+cosB}{sinB-cosB}\) b. Tính chiều cao của hình thang ABCD
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a
Tính chiều cao của hình thang ABCD
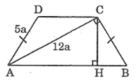
Bài 1: Cho hình thang ABCD có 2 cạnh bên AD và Bc bằng nhau, đường chéo AC vuông góc với cạnh bên BC/ Biết rằng AD 5a. AC 12aa) Tính frac{SinB+Ctext{os}B}{SinB-CosB}b) Tính chiều cao hình thăng ABCDBài 2: Cho tam giác ABC cân tại A, ABAC10cm, BC 16cm. Trên ường cao AH lấy điểm I sao cho Ai frac{1}{3}AH. Vẽ tia CX cắt tia BI tại D.a) Tính các góc tam giác ABCb) Tính diện tích tứ giác ABCD
Đọc tiếp
Bài 1: Cho hình thang ABCD có 2 cạnh bên AD và Bc bằng nhau, đường chéo AC vuông góc với cạnh bên BC/ Biết rằng AD= 5a. AC = 12a
a) Tính \(\frac{SinB+C\text{os}B}{SinB-CosB}\)
b) Tính chiều cao hình thăng ABCD
Bài 2: Cho tam giác ABC cân tại A, AB=AC=10cm, BC = 16cm. Trên ường cao AH lấy điểm I sao cho Ai = \(\frac{1}{3}AH\). Vẽ tia CX cắt tia BI tại D.
a) Tính các góc tam giác ABC
b) Tính diện tích tứ giác ABCD
Cho hinh thang ABCD co canh ben AD va BC bang nhau duong cheo AC vuong goc voi Canh BC,AD=5a,AC=12a
a)\(\frac{sinB+cosB}{sinB-cosB}\)
b) Tính chiều cao của hình thang ABCD
cho hình thang ABCD có hai cạnh bên AD VÀ BC băng nhau đường cheo AC vuông góc với cạnh bên BC biết AD=5a,AC=12a .tính chiều cao hình thang và\(\frac{sinB+cosB}{SinB-cosB}\)
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 3a, AC = 4a.
a) Tính (sin B + cos B)b) Tính chiều cao của hình thang ABCD.Bài 1: cho hình thang ABCD có 2 cạnh bên AD và BC bằng nhau, đường chéo AC vuông góc với BC biết AD5a, AC12aa) tính frac{sin B+cos B}{sin B-cos B}b)tính chiều cao của hình thang ABCDBài 2: cho tam giác cân ABC có AB AC 10cm, BC 16cm, trên đường cao AH lấy I sao cho AI 1/3 AH. Kẻ CX song song với AH, CX cắt BI tại D.a) tính các góc của tam giác ABCb) tính diện tích ABCDBài 3: cho hình thang đáy nhỏ 15 cm, 2 cạnh bên bằng nhau và bằng 25cm, góc tù là 120 độ. tính chu vi và diện tích
Đọc tiếp
Bài 1: cho hình thang ABCD có 2 cạnh bên AD và BC bằng nhau, đường chéo AC vuông góc với BC biết AD=5a, AC=12a
a) tính \(\frac{\sin B+\cos B}{\sin B-\cos B}\)
b)tính chiều cao của hình thang ABCD
Bài 2: cho tam giác cân ABC có AB = AC =10cm, BC = 16cm, trên đường cao AH lấy I sao cho AI= 1/3 AH. Kẻ CX song song với AH, CX cắt BI tại D.
a) tính các góc của tam giác ABC
b) tính diện tích ABCD
Bài 3: cho hình thang đáy nhỏ 15 cm, 2 cạnh bên bằng nhau và bằng 25cm, góc tù là 120 độ. tính chu vi và diện tích
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a.
a) Tính (sin B + cos B)/(sin B - cos B)b) Tính chiều cao của hình thang ABCD.Giúp mình với! Cảm ơn!