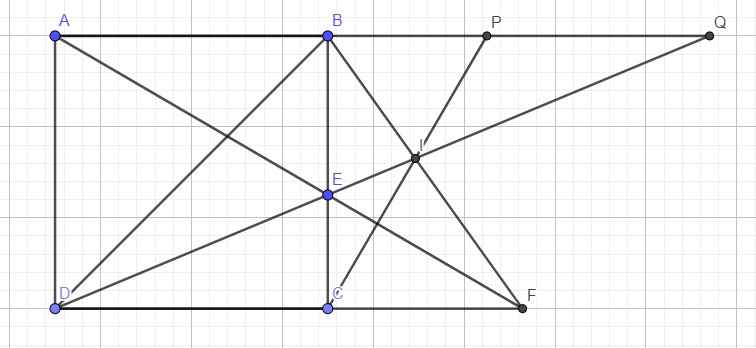
bạn ơi vậy không có số đo góc , chiều dài , chiều rộng gì à bạn
Gọi P và Q lần lượt là giao điểm của CI và DE với AB
Áp dụng talet: \(\left\{{}\begin{matrix}\dfrac{PQ}{CD}=\dfrac{IP}{IC}\\\dfrac{IP}{IC}=\dfrac{BP}{CF}\end{matrix}\right.\) \(\Rightarrow\dfrac{PQ}{CD}=\dfrac{BP}{CF}\Rightarrow\dfrac{PQ}{BP}=\dfrac{CD}{CF}=\dfrac{AB}{CF}\)
Vẫn Talet: \(\left\{{}\begin{matrix}\dfrac{AB}{CF}=\dfrac{BE}{CE}\\\dfrac{BE}{CE}=\dfrac{EQ}{DE}\end{matrix}\right.\) \(\Rightarrow\dfrac{AB}{CF}=\dfrac{EQ}{DE}\)
\(\Rightarrow\dfrac{PQ}{BP}=\dfrac{EQ}{DE}\)
\(\Rightarrow EP||CD\)
\(\Rightarrow EP\perp AC\)
\(\Rightarrow E\) là trực tâm tam giác ACP
\(\Rightarrow AE\) là đường cao thứ 3 hay \(AE\perp CP\) (đpcm)