Do ABCD là hình vuông có M, N, P, Q lần lượt là trung điểm của BC, CD, DA, AB nên: AQ = QB = BM = MC= CN = ND = DP = PA
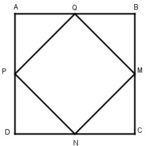
Xét Δ APQ và Δ BQM:
AQ = BM (gt)
∠ A = ∠ B = 90 0
AP = BQ (gt)
Do đó: △ APQ = △ BQM (c.g.c) ⇒ PQ = QM (1)
Xét △ BQM và △ CMN:
BM = CN (gt)
∠ B = ∠ C = 90 0
BQ = CM (gt)
Do đó: △ BQM = △ CMN (c.g.c) ⇒ QM = MN (2)
Xét △ CMN và △ DNP:
CN = DP (gt)
∠ C = ∠ D = 90 0
CM = DN (gt)
Do đó: △ CMN = △ DNP (c.g.c) ⇒ MN = NP (3)
Từ (1), (2) và (3) suy ra: MN = NP = PQ = QM
nên tứ giác MNPQ là hình thoi
Vì AP = AQ nên △ APQ vuông cân tại A
BQ = BM nên △ BMQ vuông cân tại B
⇒ ∠ (AQP) = ∠ (BQM) = 45 0
∠ (AQP) + ∠ (PQM) + ∠ (BQM) = 180 0 (kề bù)
⇒ ∠ (PQM) = 180 0 - ( ∠ (AQP) + ∠ (BQM) )
= 180 0 - ( 45 0 + 45 0 ) = 90 0
Vậy tứ giác MNPQ là hình vuông.

