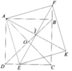
a) DDAE = DBAF (c.g.c)
⇒ D A E ^ = B A F ^ và AE = AF
Mà E A D ^ + E A B ^ = 90 0 = > E A B ^ + B A F ^ = 90 0
Þ DAEF vuông cân tại A.
b) DEAF vuông cân nên IA = IE = FI (1); DCFE vuông có IC là đường trung tuyến Þ IE = IC = IF (2);
Từ (1) và (2) suy ra Þ IA = IC nên I thuộc trung trực của AC hay I thuộc BD.
c) Do K đối xứng với A qua I nên I là trung điểm của AK.
Mà I là trung điểm của EF(gt) nên AFKE là hình bình hành, DAEF vuông cân tại A nên AI ^ EF.
Vậy AFKE là hình vuông.