Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD trên đoạn AC lấy M sao cho AC=4AM và N là trung điểm cạnh CD
CMR: Tam giác BMN là tam giác vuông cân
Cho hình chữ nhật ABCD. Kẻ BK⊥AC. Gọi M,N lần lượt là trung điểm của AK và CD
Chứng minh: (BMN) ̂=90^0. Tìm điều kiện của hình chữ nhật để tam giác BMN vuông cân.
Cho hình vuông ABCD, M thuộc AC sao cho AM=1/4AC., N là trung điểm DC.cmr tam giac BMN vuông cân (cm theo vecto)
Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho AM AC/4, N là trung điểm của đoạn thẳng DC. Tìm mệnh đề đúng? A. Tam giác BMN là tam giác vuông B. Tam giác BMN là tam giác cân C. Tam giác BMN là tam giác đều D. Tam giác BMN là tam giác vuông cân
Đọc tiếp
Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho AM = AC/4, N là trung điểm của đoạn thẳng DC. Tìm mệnh đề đúng?
A. Tam giác BMN là tam giác vuông
B. Tam giác BMN là tam giác cân
C. Tam giác BMN là tam giác đều
D. Tam giác BMN là tam giác vuông cân
Cho hình bình hành ABCD. Gọi M, N là các điểm nằm trên các cạnh AB và CD sao cho AM AB, CN CD. Gọi G là trọng tâm của tam giác BMN. Hãy phân tích theo hai vecto .
Đọc tiếp
Cho hình bình hành ABCD. Gọi M, N là các điểm nằm trên các cạnh AB và CD sao cho AM =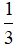 
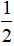
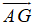
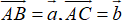
AB, CN = 
CD. Gọi G là trọng tâm của tam giác BMN. Hãy phân tích 
theo hai vecto 
.
Cho hình vuông ABCD có M là trung điểm của cạnh AB, N thuộc đoạn AC sao cho NA=3NC.
Chứng minh tam giác DMN vuông cân tại N?
Tính độ dài cạnh hình vuông biết MN=\(\sqrt{10}\) ?
Cho tam giác ABC cân tại A, M trung điểm BC, H là hình chiếu của M trên AC , E là trung điểm MH . Chứng minh AE vuông góc với BH
NA
18 tháng 8 2023 lúc 20:22
Cho tam giác ABC. Trên đoạn BC lấy điểm D sao cho CD=BC/3, trên đoạn AC lấy điểm E sao cho CE=AC/6 . Dựng hình bình hành DCEF. Trên tia FB lấy điểm M sao cho FM=2FB , trên tia FC lấy điểm N sao cho FN=3FC. Chứng minh rằng F là trọng tâm của tam giác AMN.
Cho tam giác ABC, gọi D là điểm trên cạnh BC sao cho vecto BD=2/3 vecto BC và I là trung điểm của AD. Gọi M là điểm thỏa mãn vecto AM=2/5 vecto AC. Chứng minh B,I,M thẳng hàng
Cho tam giác ABC, gọi D là điểm trên cạnh BC sao cho vecto BD=2/3 vecto BC và I là trung điểm của AD. Gọi M là điểm thỏa mãn vecto AM=2/5 vecto AC. Chứng minh B,I,M thẳng hàng