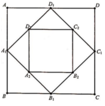
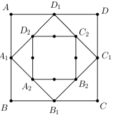
Cho hình vuông ABCD có cạnh bằng a và có diện tích S 1 . Nối 4 trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S 2 . Tiếp tục làm như thế ta được hình vuông thứ ba A 2 B 2 C 2 D 2 có diện tích S 3 …. Và cứ tiếp tục làm như thế ta được các hình vuông có diện tích S 4 , S 5 …, S 100 (tham khảo hình vẽ bên). Tính tổng S = S 1 + S 2 + S 3 + ... + S 100 .
A. S = a 2 2 100 − 1 2 100 .
B. S = a 2 2 100 − 1 2 99 .
C. S = a 2 2 100 .
D. S = a 2 2 99 − 1 2 99 .
Đáp án B.
Phương pháp:
Nếu u n là một cấp số nhân với công bội q ≠ 1 thì S n được tính theo công thức: S n = u 1 1 − q n 1 − q .
Cách giải:
Hình vuông ABCD cạnh a ⇒ S 1 = a 2
Hình vuông A 1 B 1 C 1 D 1 có cạnh bằng a 2 ⇒ S 2 = a 2 2
Hình vuông A 2 B 2 C 2 D 2 có cạnh bằng
a 2 2 = a 2 2 ⇒ S 3 = a 2 2 2
……
Hình vuông A 99 B 99 C 99 D 99 có cạnh bằng a 2 99 ⇒ S 100 = a 2 2 99
S = S 1 + S 2 + S 3 + ... + S 100 = a 2 2 0 + a 2 2 1 + a 2 2 2 + ... + a 2 2 99 = a 2 . 1 − 1 2 100 1 − 1 2 = a 2 2 100 − 1 2 100 .2 = a 2 2 100 − 1 2 99