Đáp án cần chọn là: C
Từ hình vẽ ta thấy: Điểm M nằm ngoài tứ giacsABCD và điểm N nằm trong tứ giác ABCD.
Đáp án cần chọn là: C
Từ hình vẽ ta thấy: Điểm M nằm ngoài tứ giacsABCD và điểm N nằm trong tứ giác ABCD.
Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:
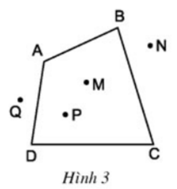
a) Hai đỉnh kề nhau: A và B, …
Hai đỉnh đối nhau: A và C, …
b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, …
c) Hai cạnh kề nhau: AB và BC, …
Hai cạnh đối nhau: AB và CD, …
d) Góc: ∠A , …
Hai góc đối nhau: ∠A và ∠C , …
e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, …
Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …
Cho tứ giác ABCD. Vẽ hình đối xứng với tứ giác ABCD qua :
a ) Qua điểm O nằm ngoài tứ giác
b ) Điểm A
c ) Qua đường thẳng d không cắt các cạnh của tứ giác.
d ) Qua AB
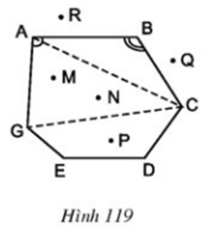
Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong các câu sau:
Các đỉnh là các điểm: A, B, …
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc …
Các cạnh là các đoạn thẳng: AB, BC, …
Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, …
Các góc là: ∠A , ∠B , …
Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, …
Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, …
Cho hình vuông ABCD. có cạnh bằng 16cm, O là giao điểm của AC và BD. Gọi M,N,P,Q lần lượt là trung điểm của OA,OB,OC,OD
a) Tứ giác MNPQ là hình j vì sao
b) Tính S hình vuông ABCD nằm ngoài tứ gics MNPQ
Cho tứ giác ABCD. gọi M,N,P,Q lần lượt là trug điểm của AB,BC,CD,DA. O là trung điểm nằm trong tứ giác. Vẽ các điểm A',B',C',D' sao cho M,N,P,Q là trung điểm OA,OB',OC',OD'. Chứng minh BB'C'D là hình bình hành.
Bác nào có tâm vẽ giúp em luôn cái hình :>
cho hình chữ nhật ABCD. Góc A được chia thành 3 góc bằng nhau bởi các tia AM và AN trong đó M nằm trên cạnh BC sao cho BM=2cm, N là trung điểm CD. Tính diện tích tứ giác ABCD
Bài 5: Cho hình bình hành ABCD. Trên đưởng chéo AC chọn hai điểm E và F sao
cho AE=EF=FC.
a) Tứ giác BEDF là hình gì?
b) Chứng minh tam giác CFD= tam giác AEB
c) Chứng minh tam giác CFB= tam giác EAD
Bài 7: Cho tam giác ABC có AB=6, AC=8, BC=10.
a) Xác định D sao cho BDCA là hình vuông.
b) Tính độ dài DA.
c) Tính diện tích ABCD.
Bài 8: Cho hình thang ABCD. Hai đường chéo AC và BD cắt nhau tại O.
a) Xác định O để ABCD là hình bình hành.
b) Hình bình hành ABCD cần thêm điều kiện gì để trở thành hình thoi.
c) Cho hình thoi ABCD có góc ABC=90 0 . Hỏi tứ giác ABCD đã trở thành hình
gì?
Bài 10: Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Gọi D, E là các hình
chiếu của H trên AB, AC và M, N theo thứ tự là các trung điểm của các đường thẳng
BH, CH.
a) Chứng minh tứ giác MDEN là hình thang vuông.
b) Gọi P là giao điểm của đường thẳng DE với đường cao AH và Q là trung điểm
của đường thẳng MN. Chứng minh PQ vuông góc DE.
c) Chứng minh hệ thức 2PQ = MD + NE.
Bài 13: Qua đỉnh A của hình vuông ABCD ta kẻ hai đường thẳng Ax, Ay vuông góc
với nhau. Ax cắt cạnh BC tại điểm P và cắt tia đối của tia CD tại điểm Q. Ay cắt tia
đối của tia BC tại điểm R và cắt tia đối của tia DC tại điểm S.
a) Chứng minh các tam giác APS, AQR là các tam giác cân.
b) Gọi H là giao điểm của QR và PS; M, N theo thứ tự là trung điểm của QR, PS.
Chứng minh tứ giác AMHN là hình chữ nhật.
Bài 14: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CA,
AD.
a) Tứ giác MNPQ là hình gì?
b) Gọi M là trung điểm của DB, AD=6, AB=8. Cho DBAM. Tính QM.
Bài 15: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB và AC.
a) Tứ giác BMNC là hình gì? Vì sao?
b) Lấy điểm E đối xứng với M qua N. Chứng minh tứ giác AECM là hình bình
hành.
c) Tứ giác BMEC là hình gì? Vì sao?
d) Tam giác ABC cần thêm điều kiện gì thì tứ giác AECM là hình vuông? Vẽ
hình minh hoạ.
Mong mn giúp mk vs ah
Bài 1: Cho tam giác ABC cân tại A có BC = 4cm. Hai điểm D và E lần lượt nằm trên cạnh AC và AB sao cho AD = 2DC, AE=2EB và BD,Ce vuông góc với nhau. Tính diện tích tam giác ABC.
Bài 2: Cho tứ giác ABCD. Qua trung điểm M của đường chéo BD dựng đường thẳng // AC cắt AD tại E. Chứng minh CE chia tứ giác ABCD thành 2 phần có diện tích bằng nhau.
2. Cho tứ giác ABCD. Lấy điểm M tùy ý trên cạnh AB xác định điểm N trên cạnh DC sao cho MN chia tứ giác ABCD thành hai phần có diện tích bằng nhau.
Hình bình hành ABCD có 4 đỉnh lần lượt nằm trên các cạnh tứ giác EFGH, trong đó có 2 điểm là trung điểm của 2 cạnh tứ giác. Chứng minh diện tích hình bình hành ABCD = \(\frac{1}{2}\)diện tích tứ giác EFGH