Đáp án là C
∠(BEC) là góc có đỉnh nằm trong đường tròn
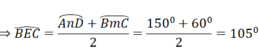
Đáp án là C
∠(BEC) là góc có đỉnh nằm trong đường tròn
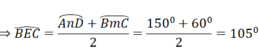
Trên đường tròn tâm O bán kính R lấy hai điểm A và B sao cho AB = R. Số đo góc
AOB chắn cung nhỏ AB có số đo là :
A.30 0 B. 60 0 C. 90 0 D . 120 0

1.Trong hình 1, biết AC là đường kính, góc BDC bằng 600. Số đo góc ACB bằng
A. 400. | B. 450. | C. 350. | D. 300. |
2.Trong hình 2, góc QMN bằng 600, số đo góc NPQ bằng
A. 200. | B. 250. | C. 300. | D. 400. |
3.Trong hình 3, AB là đường kính của đường tròn, góc ABC bằng 600, khi đó số đo cung BmC bằng
A. 300. | B. 400. | C. 500. | D. 600. |
4.Trong hình 4, biết AC là đường kính của đường tròn, góc ACB bằng 300. Khi đó số đo góc CDB bằng
A. 400. | B. 500. | C. 600. | D. 700. |

5.Trên hình 5, biết số đo cung AmD bằng 800, số đo cung BnC bằng 300. Số đo của góc AED bằng
A. 250. | B. 500. | C. 550. | D. 400. |
6.Trong hình 6, số đo góc BIA bằng 600, số đo cung nhỏ AB bằng 550. Số đo cung nhỏ CD là
A. 750. | B. 650. | C. 600. | D. 550. |
7.Trên hình 7, có MA, MB là các tiếp tuyến tại A và B của (O). Số đo góc AMB bằng 580. Khi đó số đo góc OAB là
A. 280. | B. 290. | C. 300. | D. 310. |
8.Trên hình 8, số đo góc QMN bằng 200, số đo góc PNM bằng 100. Số đo của góc x bằng
A. 150. | B. 200. | C. 250. | D. 300 |

9.Trên hình 9, số đo cung nhỏ AD bằng 800. Số đo góc MDA bằng
A. 400. | B. 500. | C. 600. | D. 700. |
10.Trong hình 10, MA, MB là tiếp tuyến của (O), BC là đường kính, góc BCA bằng 700. Số đo góc AMB bằng
A. 700. | B. 600. | C. 500. | D. 400. |
11.Trong hình 11, có góc BAC bằng 200, góc ACE bằng 100, góc CED bằng 150. Số đo góc BFD bằng
A. 550. | B. 450. | C. 350. | D. 250. |
12.Trong hình 12, có AD//BC, góc BAD bằng 800, góc ABD bằng 600. Số đo góc BDC bằng
A. 400. | B. 600. | C. 450. | D. 650. |
1. Cho đường tròn ( 0 ; R ) . Một điểm A ở đó bên ngoài đường tròn sao cho OA = 2R . Vẽ các tiếp tuyến AB và AC đến (0) ( A,B là 2 tiếp điểm )
a) Tính số đo các góc AOB và BOC
b) Tính số đo cung nhỏ và cung lớn BC
Giúp em với ạ , em đang cần gấp lắm !
Cho tam giác ABC nội tiếp (O). Tiếp tuyến tại A của (O) cắt BC tại P
a) Giả sử (BCA) ̂=〖30〗^0. Tính số đo cung nhỏ và cung lớn AB, số đo (PAB) ̂ , số đo (AOB) ̂
b) Chứng minh
c) Tia phân giác trong góc A cắt BC và (O) lần lượt tại D và M. Chứng minh:
MB
Cho tam giác ABC nội tiếp (O). Tiếp tuyến tại A của (O) cắt BC tại P a) Giả sử (BCA) ̂=〖30〗^0. Tính số đo cung nhỏ và cung lớn AB, số đo (PAB) ̂ , số đo (AOB) ̂ b) Chứng minh c) Tia phân giác trong góc A cắt BC và (O) lần lượt tại D và M. Chứng minh: MB
Cho (0 ; R) đường kính AB. Vẽ dây cung CD =R, AC và BD kéo dài cắt nhau tại e A) tính số đo cung CD nhỏ và số đo góc AEB B) GỌI H LÀ GIAO ĐIỂM CỦA AD VÀ BC, CM TỨ GIÁC ACHD NỘI TIẾP C) CHỨNG MINH A H + AD + BC + BC = 4 R
* Cho ΔABC có BC=12cm, góc B=\(60^0\), góc C=\(40^0\)
a. Tính đường cao CH và cạnh AC
b. Tính diện tích ΔABC (làm tròn đến chữ số thập phân thứ 2)
* Cho ΔABC vuông tại A có góc B= \(30^0\), AB=6cm
a. Giải tam giác vuông ABC
b. Vẽ đường cao AH, trung tuyến AM của ΔABC. Tính diện tích ΔAHM
Cho tam giác ABC vuông ở A, có góc B = 200 . Vẽ phân giác trong BI, vẽ góc ACH = 300 về phía trong tam giác. Tính số đo góc CHI
Bài 1. Cho tam giác ABC cân tại A nội tiếp đường tròn (O) và 𝐴= 𝑎(0 < 𝑎 < 90). Gọi M là một điểm tuỳ ý trên cung nhỏ AC. Vẽ tia Bx vuông góc AM, cắt tia CM tại D.
a) Tính số đo góc 𝐴𝑀D b) Chứng minh rằng MD = MB.