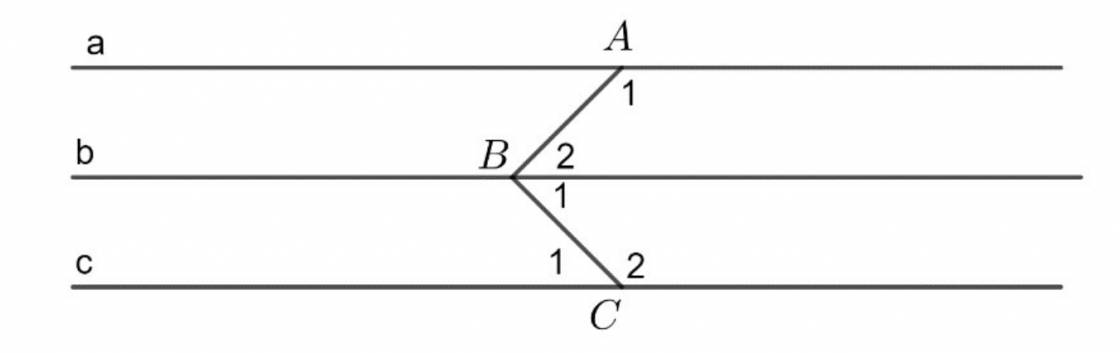
a) Ta có: ˆA1+ˆA2=1800A1^+A2^=1800 ( Vì kề bù )
⇒ˆA2=1800−ˆA1⇒A2^=1800−A1^
Thay số: ˆA2=1800−700=1100A2^=1800−700=1100
⇒ˆB1=ˆA2=1100⇒B1^=A2^=1100
⇒b//a⇒b//a( Vì có 2 góc ˆB1=ˆA2=1100B1^=A2^=1100ở vị trí đồng vị )
Ta có: ˆB1+ˆB2=1800B1^+B2^=1800 ( Vì kề bù )
⇒ˆB2=1800−ˆB1⇒B2^=1800−B1^
Thay số: ˆB2=1800−1100=700B2^=1800−1100=700
⇒ˆC1=ˆB2=700⇒C1^=B2^=700
⇒b//c⇒b//c ( Vì có 2 góc ˆC1=ˆB2=700C1^=B2^=700ở vị trí đồng vị )
Mà b//ab//a ( Chứng minh trên )
⇒a//b//c⇒a//b//c
b) Ta có: ˆF1+ˆF2=1800F1^+F2^=1800 ( Vì kề bù )
⇒ˆF1=1800−ˆF2⇒F1^=1800−F2^
Thay số: ˆF1=1800−800=1000F1^=1800−800=1000
Mà b//c⇒ˆF1=ˆE1=1000b//c⇒F1^=E1^=1000 ( Vì sole ngoài )
Và a//b⇒ˆD1=ˆE1=1000a//b⇒D1^=E1^=1000 ( Vì sole trong )
⇒ˆD1+ˆE1+ˆF1=1000+1000+1000=3000⇒D1^+E1^+F1^=1000+1000+1000=3000
c) AH⊥cAH⊥c ( gt )
Và a//b//ca//b//c
⇒AH⊥a;AH⊥b⇒AH⊥a;AH⊥b
d) Ta có: ˆD1=ˆE1=1000D1^=E1^=1000 ( Theo chứng minh phần b )
⇒⇒ Phân giác của ˆD1D1^ = Phân giác của ˆE1E1^
Hay ˆD2=ˆD3=ˆE2=ˆE3=10002=500D2^=D3^=E2^=E3^=10002=500
⇒⇒ Phân giác của ˆD1D1^ // Phân giác của ˆE1E1^ ( Vì có 2 góc ˆD2=ˆE2=500D2^=E2^=500 ở vị trí sole trong )
bài này có sai ko đấy bn