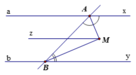
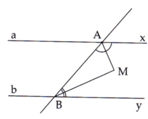
Kẻ M z / / a x / / b y
Vì AM là tia phân giác của x A B ^
⇒ A M z ^ = x A M ^ = 1 2 x A B ^
BM là phân giác của A B y ^
⇒ A B M ^ = M B y ^ = 1 2 A B y ^
Ta có: M z / / a x nên A M z ^ = M A x ^ (hai góc so le trong)
M z / / b y nên z M B ^ = B M y ^ (hai góc so le trong)
⇒ A M B ^ = A M z ^ + z M B ^ = 1 2 x A B ^ + A B y ^ = 1 2 ⋅ 180 0 = 90 0
Vậy A M ⊥ B M (đpcm)