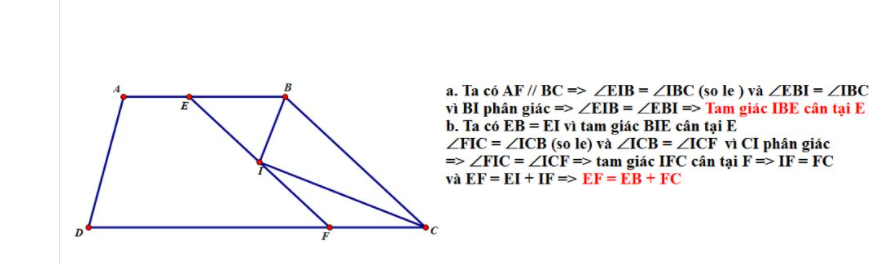
\(a,\) Ta có \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right);\widehat{B_2}=\widehat{I_1}\left(so.le.trong.do.EI//BC\right)\)
\(\Rightarrow\widehat{B_1}=\widehat{I_1}\Rightarrow\Delta BEI.cân.tại.E\)
Ta có \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right);\widehat{C_2}=\widehat{I_2}\left(so.le.trong.do.FI//BC\right)\)
\(\Rightarrow\widehat{C_1}=\widehat{I_1}\Rightarrow\Delta CFI.cân.tại.F\)
\(b,\) Vì \(\Delta BEI.và.\Delta CFI\) cân nên \(\left\{{}\begin{matrix}BE=EI\\CF=FI\end{matrix}\right.\)
\(\Rightarrow BE+CF=EI+FI=EF\)
Các hình thang: BEFC do EF//BC; ADFE do AE//DF; ABCD do giả thiết