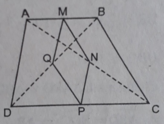
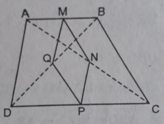
Hình thang ABCD là hình thang cân có hai góc kề một đáy đều bằng 45 0 thì MNPQ là hình vuông.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình thang ABCD ( AB//CD). Gọi M;N;P;Q theo thứ tự là trung điểm của các cạnh AB;AC;CD;BD.
a/ Tứ giác MNPQ là hình gì?
b/ Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi?
c/ Khi ABCD là hình thang cân có hai đường chéo vuông góc thì MNPQ là hình gì?
Cho hình thang ABCD (AB//CD). Gọi MNPQ theo thứ tự là trung điểm của AB, AC ,CD,BD
a, chứng minh rằng MNPQ là hình bình hành
b, Nếu ABCD là hình thang cân thì tứ giác MNPQ là hình gì? VÌ sao?
c, HÌnh thang ABCD có thêm điều kiện gì thì MNPQ là hình vuông
Cho hình thang ABCD. Gọi M,N,P,Q lần lượt là trung điểm của AB,AC,CD,BD. Hình thang ABCD có thêm điều kiện gì thì MNPQ là hình vuông?
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD. Nếu ABCD là hình thang cân thì tứ giác MNPQ là hình gì? Vì sao?
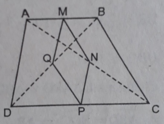
Cho hình thang ABCD ( AB//CD). GọiM,N,P,Q lần lượt là các trung điểm của các cạnh AB,AC,CD,BD
a)Tứ giác MNPQ là hình gì ? Vì sao ?
b)Nếu tứ giác ABCD là hình thang cân thì tứ giác MNPQ là hình gì ? Vì sao ?
c)Hình thang ABCD có thêm điều kiện gì để tứ giác MNPQ là hình vuông.
cho hình thang ABCD (AB//BD).Gọi M,N,P,Q theo thứ tự là trung điểm của AB,AC,CD,BD.
a) Chứng minh rằng MNPQ là hình binh hành?
b)nếu ABCD là hình thang cân thì tứ giác MNPQ là hình gì?Vì sao?
Cho hình thang ABCD (AB//CD.Gọi E,F theo thứ tự là trung điểm của AB,CD. Gọi O là trung điểm của EF. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự ở M và N
a, Tứ giác EMFN là hình gì ? Vì sao?
b, Hình thang ABCD có thêm điều kiện gì thì EMFN là hình thoi?
c, Hình thang ABCD có thêm điều kiện gì thì EMFN là hình vuông?
cho hình thanh ABCD có đáy nhỏ là AB, Gọi MNPQ lần lượt là trung điểm của AB AC CD BD
a)CMR:MNPQ là hbh
b)nếu từ giác ABCD là hình thang cân thì PM là phân giác của NPQ
c)hình thang ABCD cần thêm điều kiện gì để MNPQ là hình vuông
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD. Chứng minh rằng MNPQ là hình bình hành.