Các câu hỏi tương tự
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB và EG? A.
90
o
B.
60
o
C.
45
o
D.
120
o
Đọc tiếp
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB và EG?
A. 90 o
B. 60 o
C. 45 o
D. 120 o
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).
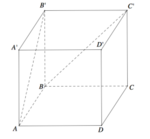
A. 60 °
B. 90 °
C. 45 °
D. 300 °
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên). A.
60
°
B.
90
°
C.
45
°
D.
30
°
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).

A. 60 °
B. 90 °
C. 45 °
D. 30 °
Cho khối chóp tứ giác đều P.ABCD có tất cả các cạnh bằng 2 được đặt nằm bên trên khối lập phương ABCD.EFGH (như hình vẽ). Côsin góc giữa hai mặt phẳng (PAB) và (AEFB) bằng A.
6
3
B.
3
3
C.
2
2
3
D. ...
Đọc tiếp
Cho khối chóp tứ giác đều P.ABCD có tất cả các cạnh bằng 2 được đặt nằm bên trên khối lập phương ABCD.EFGH (như hình vẽ). Côsin góc giữa hai mặt phẳng (PAB) và (AEFB) bằng
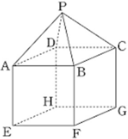
A. 6 3
B. 3 3
C. 2 2 3
D. 1 3
Cho hình lăng trụ ABCD.ABCD có đáy là hình thoi cạnh bằng a và
A
B
C
⏜
120
°
. Góc giữa cạnh bên AA và mặt đáy bằng
60
°
, điếm A’ cách đều các điểm A, B, D . Tính thể tích khối lăng trụ đã cho theo a. A.
a
3
3
3...
Đọc tiếp
Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình thoi cạnh bằng a và A B C ⏜ = 120 ° . Góc giữa cạnh bên AA' và mặt đáy bằng 60 ° , điếm A’ cách đều các điểm A, B, D . Tính thể tích khối lăng trụ đã cho theo a.
A. a 3 3 3
B. a 3 3 2
C. a 3 3 12
D. a 3 3 6
Cho hình lập phương ABCD. A 'B 'C 'D ' có I, J tương ứng là trung điểm của BC và BB ' . Góc giữa hai đường thẳng AC và IJ bằng
A. 45 °
B. 60 °
C. 30 °
D. 120 °
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng A.
10
5
B.
4
5
C.
10
10
D.
2
5
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng
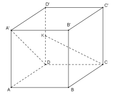
A. 10 5
B. 4 5
C. 10 10
D. 2 5
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Gọi M là trung điểm cạnh DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CB′ và MC′ bằng A.
2
2
9
B.
10
10
C.
2
9
D.
10
5
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Gọi M là trung điểm cạnh DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CB′ và MC′ bằng
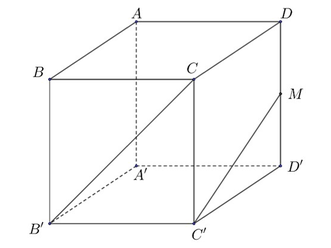
A. 2 2 9
B. 10 10
C. 2 9
D. 10 5
Cho hình chóp tam giác S.ABC có
S
A
a
;
S
B
b
;
S
C
c
và
B
S
C
⏜
120
°
,
C
S
A
⏜
90...
Đọc tiếp
Cho hình chóp tam giác S.ABC có S A = a ; S B = b ; S C = c và B S C ⏜ = 120 ° , C S A ⏜ = 90 ° , A S B ⏜ = 60 ° . Gọi G là trọng tâm của tam giác ABC. Độ dài đoạn SG bằng
A. 1 3 a 2 + b 2 + c 2 + a b + b c + c a
B. a 2 + b 2 + c 2 + a b - b c
C. 1 3 a 2 + b 2 + c 2 + a b - c a
D. 1 3 a 2 + b 2 + c 2 + a b - b c


