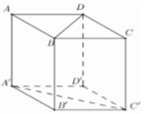
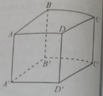
Kẻ B'D' vuông A'C' do tứ giác A'B'C'D' là hình vuông
Cho B'D' giao A'C' tại O
Từ O kẻ OH vuông A'C'
Ta có A'C' vuông B'O; AA' vuông B;O; AA', A'C' chứa (AA'CC')
=> B'O vuông (AA'C'C)
=> B'O vuông A'C
Lại có OH vuông A'C
=> A'C vuông (B'OH)
=> A'C vuông B'H
tương tự cm được A'C vuông D'H
=> góc nhị diện [B',A'C,D'] là góc ^B'HD'
Cho các cạnh hình lập phương là a
Xét tam giác A'B'C vuông tại B' do A'B' vuông (BB'CC') => A'B' vuông B'C
\(\dfrac{1}{B'H^2}=\dfrac{1}{A'B'^2}+\dfrac{1}{B'C^2}=\dfrac{1}{a^2}+\dfrac{1}{2a^2}=\dfrac{3}{2a^2}\Rightarrow B'H=\sqrt{\dfrac{2}{3}}a\)
tương tự \(D'H=\sqrt{\dfrac{2}{3}}a\)
Ta có B'D' = \(\sqrt{2}a\)
cos^B'HD' = \(\dfrac{B'H^2+HD'^2-B'D'^2}{2.B'H.HD'}\Rightarrow\widehat{B'HD'}=120^0\)