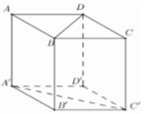
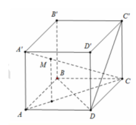
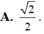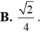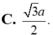Cho O là giao điểm A'C' và B'D'
Ta có BB' vuông A'C' ; B'O vuông A'C'
=> A'C' vuông (BB'O)
=> A'C' vuông BO
Ta có BO vuông A'C' ; B'O vuông A'C'
=> góc nhị diện [B',A'C',B'] là ^BOB'
Cho 1 cạnh hình lập phương là a
Xét tam giác BB'O vuông tại B'
tanbeta = \(\dfrac{BB'}{BO}=\dfrac{a}{\dfrac{\sqrt{2}a}{2}}=\sqrt{2}\)
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A’C và MN.
Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa các cặp đường thẳng sau đây:
a) AB và B’C’
b) AC và B’C’
c) A’C’ và B’C
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và A’C’ là:
Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của AA’ và CD. Góc giữa hai đường thẳng BM và C’N bằng:
A. 45 0
B. 30 0
C. 60 0
D. 90 0
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi α là góc giữa đường thẳng A’B và mặt phẳng (BB’D’D). Tính sin α.
A. 3 4
B. 3 2
C. 3 5
D. 1 2
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi α là góc giữa đường thẳng AB’ và mặt phẳng (BB’D’D) Tính sin α
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích S của mặt cầu ngoại tiếp hình lập phương ABCD.A’B’C’D’
A. S = πa 2
B. S = 3 πa 2
C. S = πa 2 3 2
D. S = 4 πa 2 3
Gọi V là thể tích hình lập phương ABCD.A’B’C’D’, là thể tích của tứ diện A’ABD. Hệ thức nào sau đây là đúng?
A. V= 6 V 1
B. V = 4 V 1
C. V = 3 V 1
D. V = 2 V 1
Cho hình lập phương ABCD.A’B’C’D’. Gọi (P) là mặt phẳng đi qua trung điểm của AC’ và vuông góc với BB’. Ảnh của tứ giác ADC’B’ qua phép đối xứng mặt phẳng (P) là:
A. Tứ giác ADC’B’
B. Tứ giác A’B’C’D’
C. Tứ giác ABC’D’
D. Tứ giác A’D’CB
Cho hình lập phương ABCD.A’B’C’D’. Gọi M là điểm trên đường chéo CA’ sao cho 
Tính tỉ số giữa thể tích
V
1
của khối chóp M.ABCD và thể tích
V
2
của khối lập phương
