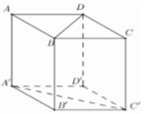
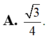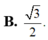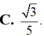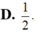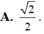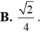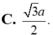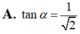Ta có CC' vuông (A'B'C'D')
=> ^(A'C;(A'B'C'D')) = ^(A'C;C'A') = ^CA'C
Cho 1 cạnh là a
Theo Pytago tam giác A'B'C' ta có
\(A'C'=\sqrt{A'B'^2+B'C'^2}=\sqrt{2}a\)
AC = \(\sqrt{2}a\)
Theo Pytago tam giác A'AC vuông tại A
\(A'C=\sqrt{AA'^2+AC^2}=\sqrt{2a^2+a^2}=\sqrt{3}a\)
Xét tam giác CA'C' vuông tại C'
tanalpha = A'C/A'C' = \(\dfrac{\sqrt{3}a}{\sqrt{2}a}=\dfrac{\sqrt{6}}{2}\)
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi α là góc giữa đường thẳng A’B và mặt phẳng (BB’D’D). Tính sin α.
A. 3 4
B. 3 2
C. 3 5
D. 1 2
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi α là góc giữa đường thẳng AB’ và mặt phẳng (BB’D’D) Tính sin α
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A’C và MN.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và A’C’ là:
Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa các cặp đường thẳng sau đây:
a) AB và B’C’
b) AC và B’C’
c) A’C’ và B’C
Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
a) Chứng minh rằng đường thẳng AC’ vuông góc với mặt phẳng (A’BD) và mặt phẳng (ACC’A’) vuông góc với mặt phẳng (A’BD).
b) Tính đường chéo AC’ của hình lập phương đã cho.
Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của AA’ và CD. Góc giữa hai đường thẳng BM và C’N bằng:
A. 45 0
B. 30 0
C. 60 0
D. 90 0
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai mặt phẳng (A’B’CD) và (ABC’D’) bằng
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SBC là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, biết \(\alpha\) là góc giữa đường thẳng SD và (SBC) và \(\sin\alpha=\frac{2\sqrt{26}}{13}\). Gọi \(\beta\)là góc giữa hai mặt phẳng (SAC) và (ABCD). Tính \(\beta\)?
Mong mọi người hướng dẫn giải! Cám ơn mọi người!
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a các mặt bên (SAB), (SAD) cùng vuông góc với mặt phẳng đáy, SA=a; góc giữa đường thẳng SC và mặt phẳng (SAB) bằng a. Khi đó tan α nhận giá trị nào trong các giá trị sau:
