Đáp án A
Phương pháp:
- Sử dụng phương pháp tọa độ hóa.
- Công thức tính khoảng cách giữa hai đường thẳng chéo nhau:
Cho ∆ có VTCP u → và qua M; ∆ ' có VTCP v → và qua M’

Cách giải:
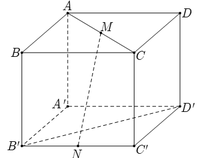
Gắn hệ trục tọa độ như hình vẽ, trong đó:
A'(0;0;0), B'(0;a;0), C'(a;a;0), D'(a;0;0)
A(0;0;a), B(0;a;a), C(a;a;a); D(a;0;a), M(a/2;a;a)
Đường thẳng AM có VTCP ![]() và qua A(0;0;a)
và qua A(0;0;a)
Đường thẳng DB’ có VTCP ![]() và qua D(a;0;a)
và qua D(a;0;a)
A D → = ( a ; 0 ; 0 )
Khoảng cách giữa hai đường thẳng AM và DB’: 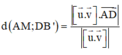
Ta có:
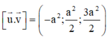
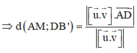

Vây, khoảng cách giữa AM và DB’ là a 2 7