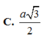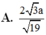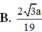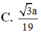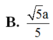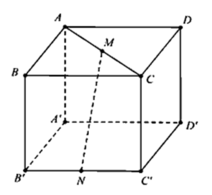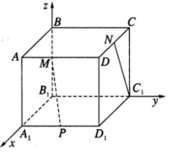
Ta chọn hệ trục tọa độ như sau: B 1 là gốc tọa độ, B 1 A 1 → = i → , B 1 C 1 → = j → , B 1 B → = k → . Trong hệ trục vừa chọn, ta có B 1 (0; 0; 0), B(0; 0; 1), A 1 (1; 0; 0), D 1 (1; 1; 0), C(0; 1; 1), D(1; 1; 1), C 1 (0; 1; 0).
Suy ra M(0; 0; 1/2), P(1; 1/2; 0), N(1/2; 1; 1)
Ta có MP → = (1; 1/2; −1/2); C 1 N → = (1/2; 0; 1)
Gọi ( α ) là mặt phẳng chứa C 1 N và song song với MP. ( α ) có vecto pháp tuyến là n → = (1/2; −5/4; −14) hay n ' → = (2; −5; −1)
Phương trình của ( α ) là 2x – 5(y – 1) – z = 0 hay 2x – 5y – z + 5 = 0
Ta có:
d(MP,
C
1
N) = d(M,(
α
)) 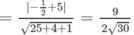
Ta có:
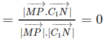
Vậy ∠ (MP, C 1 N) = 90 ° .