Đáp án là C
V = a . a 2 3 4 = a 3 3 4 .
Đáp án là C
V = a . a 2 3 4 = a 3 3 4 .
Cho khối lăng trụ tam giác đều A B C . A ' B ' C ' có cạnh đáy bằng 2, diện tích tam giác A'BC bằng 3. Tính thể tích của khối lăng trụ
A. 2 5 3
B. 2
C. 2 5
D. 3 2
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 2, diện tích tam giác A’BC bằng 3. Tính thể tích của khối lăng trụ
A. 2 5 3
B. 2
C. 2 5
D. 3 2
Cho lăng trụ tam giác đều có cạnh đáy bằng 2a và các cạnh bên đều là hình vuông. Tính theo a thể tích khối lăng trụ đã cho.
A. 2 a 3 2 3
B. 2 a 3 2
C. 2 a 3 2 4
D. 2 a 3 3
Cho một khối lăng trụ có thể tích là 3 .a 3 , đáy là tam giác đều cạnh a. Tính chiều cao h của khối lăng trụ.
A. h = 4a
B. h = 3a
C. h = 2a
D. 12a
Cho hình lăng trụ tam giác đều có tất cả các cạnh bằng a. Tính thể tích V của khối trụ ngoại tiếp hình lăng trụ
A . V = πa 3 3
B . V = a 3 3
C . V = πa 3 9
D . V = 3 a 3 π
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
A. 5 π a 2 3
B. 7 π a 2 3
C. 3 π a 2
D. 11 π a 2 3
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
A. S = 17 πa 2 13
B. S = 7 πa 2 3
C. S = 17 πa 2
D. S = 7 π a 2
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
A. 5 π a 2 3
B. 7 π a 2 3
C. 3 π a 2
D. 11 π a 2 3
Từ một mảnh giấy hình vuông cạnh a , người ta gấp thành hình lăng trụ theo hai cách sau:
- Cách 1. Gấp thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều có thể tích là V 1 (Hình 1).
- Cách 2. Gấp thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều có thể tích là V 2 (Hình 2).
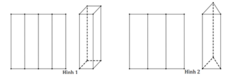
Tính tỉ số k = V 1 V 2
A. k = 3 3 8
B. k = 3 3 2
C. k = 4 3 9
D. k = 3 3 4