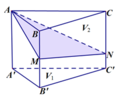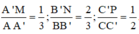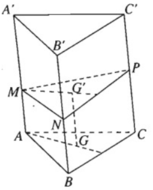
Gọi G và G' lần lượt là trọng tâm của tam giác ABC và tam giác MNP . Ta có:
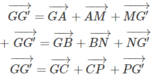
Cộng từng vế với vế ta có:
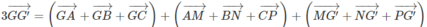
Vì G là trọng tâm của tam giác ABC nên 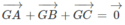
và G' là trọng tâm của tam giác MNP nên:
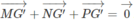
Do đó: 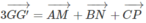
Hay 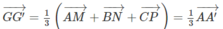
Vì điểm G cố định và 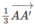 là vectơ không đổi
là vectơ không đổi
nên G' là điểm cố định. Vậy mặt phẳng (MNP) luôn luôn đi qua điểm G' cố định.