Các câu hỏi tương tự
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với ABACa và cạnh
B
A
C
⏜
120
0
, cạnh bên BBa, gọi I là trung điểm của CC’. Côsin góc tạo bởi mặt phẳng (ABC) và (AB’I) bằng: A.
20
10
B.
3
C. ...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với AB=AC=a và cạnh B A C ⏜ = 120 0 , cạnh bên BB'=a, gọi I là trung điểm của CC’. Côsin góc tạo bởi mặt phẳng (ABC) và (AB’I) bằng:
A. 20 10
B. 3
C. 30 10
D. 30 10
Cho hình lăng trụ đứng ABCABC có đáy ABC là tam giác cân,
A
B
A
C
α
,
B
A
C
^
120
°
,
B
B
α
, I là trung điểm của CC Gọi
α
là góc giữa hai mặt phẳng (ABC) và (ABI). Tính
cos
α
Đọc tiếp
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác cân, A B = A C = α , B A C ^ = 120 ° , B B ' = α , I
là trung điểm của CC' Gọi α là góc giữa hai mặt phẳng (ABC) và (AB'I). Tính cos α
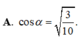
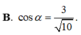

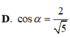
Cho lăng trụ đứng ABCABC có đáy ABC là tam giác cân, AB AC a, BAC
120
0
, BB a, I là trung điểm CC. Gọi
(
α
)
là góc giữa hai mặt phẳng (ABC) và (ABI). Tính cos
α
Đọc tiếp
Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác cân, AB = AC = a, BAC = 120 0 , BB' = a, I là trung điểm CC'. Gọi ( α ) là góc giữa hai mặt phẳng (ABC) và (AB'I). Tính cos α
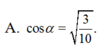
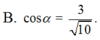
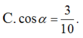
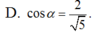
Cho lăng trụ đứng ABC.ABC có ABACBBa,
B
A
C
⏜
120
0
. Gọi I là trung điểm của CC’. Ta có cosin của góc giữa hai mặt phẳng (ABC) và (ABI) bằng:
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có AB=AC=BB'=a, B A C ⏜ = 120 0 . Gọi I là trung điểm của CC’. Ta có cosin của góc giữa hai mặt phẳng (ABC) và (AB'I) bằng:
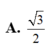
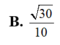
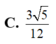
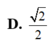
Cho lăng trụ tam giác ABC.ABC có đáy là tam giác đều cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng
30
∘
. Biết hình chiếu vuông góc của A trên (ABC) trùng với trung điểm cạnh BC. Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A.ABC
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30 ∘ . Biết hình chiếu vuông góc của A' trên (ABC) trùng với trung điểm cạnh BC. Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A'.ABC
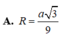
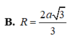
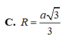
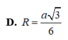
Cho lăng trụ đứng ABC. A’B’C’ có cạnh bên AA’2a, ABACa, góc
B
A
C
^
120
°
. Gọi M là trung điểm của BB’ thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC’M) là A.
3
31
B.
3
3
C.
3
15
D. ...
Đọc tiếp
Cho lăng trụ đứng ABC. A’B’C’ có cạnh bên AA’=2a, AB=AC=a, góc B A C ^ = 120 ° . Gọi M là trung điểm của BB’ thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC’M) là
A. 3 31
B. 3 3
C. 3 15
D. 93 31
Cho khối lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A với AB AC a, BAC 120
°
, mặt bên (ABC) tạ0 với mặt đáy (ABC) một góc 60
°
. Gọi M là điểm thuộc cạnh AC sao cho AM 3MC. Tính thể tích V của khối chóp CMBC A. V
a
3
32
B. V
a
3
8
C. V
a
3...
Đọc tiếp
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A với AB = AC = a, BAC = 120 ° , mặt bên (AB'C') tạ0 với mặt đáy (ABC) một góc 60 ° . Gọi M là điểm thuộc cạnh A'C' sao cho A'M = 3MC'. Tính thể tích V của khối chóp CMBC'
A. V = a 3 32
B. V = a 3 8
C. V = a 3 24
D. V = a 3 8
Cho lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại A, cạnh ACb, góc ACB
60
°
. Góc giữa đường thẳng BC và mặt phẳng (AACC) bằng 30
°
. Tính theo b diện tích xung quanh của hình lăng trụ ABC.ABC.
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, cạnh AC=b, góc ACB= 60 ° . Góc giữa đường thẳng BC' và mặt phẳng (AA'C'C) bằng 30 ° . Tính theo b diện tích xung quanh của hình lăng trụ ABC.A'B'C'.
![]()
![]()
![]()
![]()
Cho lăng trụ tam giác ABC.ABC có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A trên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Góc giữa cạnh bên của lăng trụ và mặt đáy bằng 300. Tính thể tích của lăng trụ đã cho theo a. A. 3a3/4 B. a3/4 C. a3/24 D. a3/8
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Góc giữa cạnh bên của lăng trụ và mặt đáy bằng 300. Tính thể tích của lăng trụ đã cho theo a.
A. 3a3/4
B. a3/4
C. a3/24
D. a3/8